RESEARCH ARTICLE
CP Asymmetries (& T Violation) in Known Matter – and Beyond
I.I. Bigi*
Article Information
Identifiers and Pagination:
Year: 2016Volume: 3
First Page: 1
Last Page: 22
Publisher Id: PHY-3-1
DOI: 10.2174/1874843001603010001
Article History:
Received Date: 4/7/2015Revision Received Date: 5/8/2015
Acceptance Date: 12/9/2015
Electronic publication date: 26/07/2016
Collection year: 2016
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
Abstract
Finding CP violation (CPV) in 1964 produced a real revolution in the fundamental dynamics, although the community did not understand it right away. The paper by Kobayashi & Maskawa [1] appeared in 1973 to describe CPV in classes of three (or more) families of quarks, non-minimal Higgs' dynamics and/or charged right-handed currents.
The Standard Model is now with three families of quarks. It can describe the measured CP & T violation in kaon and B mesons at least as the leading source. None has been found in baryons, charm mesons, top quarks and EDMs.
We have failed the explain our matter vs. anti-matter huge asymmetry. Even when there is no obvious connections with that asymmetry, it makes sense to probe CPV for the signs of New Dynamics & their features. Furthermore we have to measure regional CPV in many-body final states with accuracy. I discuss EDMs, axion's impact on cosmology & its connection with Dark Matter; finally I talk about CPV in leptonic dynamics.
From Roman history about data: Caelius (correspondent of Cicero) had taken a pragmatic judgment of who was likely to win the conflict and said: Pompey had the better cause, but Caesar the better army, and so I became a Caesarean.1
Obviously I am a theorist working with the tools we got from quantum mechanics & quantum field theories. I cannot express better – in one sentence – about the connection with the works of experimenters and theorists, as you see in the Fig. (1)2.
PROLOGUE
This is a short review about CP violation and with some comments about the complex scenario of time reversal. The goal is to remember ‘mature’ readers what they have heard before; for the ‘young’ ones it should show the ‘roads’ where one can learn from references in details. Furthermore we have to use tools based on local gauge symmetries. One can see the difference about local vs. discrete symmetries in real world on the Fig. (2), namely scenarios of physics vs. chemistry.
There is a very long history on our planet. It has been the goal to understand fundamental dynamics: first about ‘elements’ and then ‘elementary particles’ in more & more refined versions. Afterwards we have used the practical words of ‘high energy physics’ (HEP) instead. Somewhat recently our community realized that we might barking at the wrong tree; instead we have to think about ‘symmetries’ like local ones starting with QED and later about weak and strong forces.
There is another class of symmetries, namely discrete ones; there are subclasses:
- (i) Parity (P), charge conjugation (C) and time reversal (T);
- (ii) chiral symmetry;
- (iii) flavor symmetry.
Those discrete symmetries are correlated due to dynamics in important ways as discussed below in some details.
 |
Fig. (1). “ To be honest, I never would have invented the wheel if not for Urg's groundbreaking theoretical work with the circle.” [A long time ago I had found this cartoon on an in-flight journal.] |
 |
Fig. (2). Running with discrete symmetry. |
I focus on CP violation; on the other hand (broken) chiral and flavor symmetries have great impact on CP asymmetries. I assume that the reader knows about basic tools for quantum mechanics & quantum field theories including non-abelian ones, Einstein-Podolsky-Rosen (EPR) correlations from quantum mechanics3 and the impact of symmetries like P/C/T4.
Operators P and C are unitary, namely P†[C†] = P−1[C−1]. However the situation for the anti-unitary operator T is more subtle; one of the reasons changes initial
 final states:
final states:
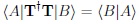 |
(1) |
CPT invariance has been assumed as usual for excellent reasons in this article.
On the other hand it can help to understand the underlying dynamics, namely Kramers’ degeneracy:
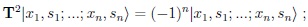 |
(2) |
1 ‘Cause’ = symmetry, yet ‘army’ = data.
2 Not all colleagues are so polite to give such credit.
3 Often the word of ‘entanglement’ has been used in this situation.
4 “All animals are equal, but some animals are more equal than others!” G. Orwell, ‘Animal Farm’.
i.e., T2 = −1 applies to a system with an odd number of the same fermions and thus ‘usable’. It also helps to understand the rules of ‘detailed balance’.
There are more general comments about CP & T asymmetries:
- This article focuses on the weak decays of kaon, charm & beauty mesons and charged lepton τ
- I mention weak decays of top quarks, but also their production in the connection with other states at very high energy collisions like Higgs states [2, 3].
- We have to continue probing CP & T asymmetries in flavor independent transitions like in electric dipole moments (EDM); non-zero number has not been found yet.
- With neutrino oscillation having been established we have a subtle, but wide landscape for New Dynamics (ND) to probe. It needs long time to achieve the goal – but there is a needed ‘price’ to reach the ‘prize’.
- History shows us there was a difference between nuclear and high energy physics; however I think that is not the best road now. In particular in Europe there are groups working between nuclear forces and HEP called Hadrodynamics. We can see the connections between the tools produced in one section and applied to others. It says it with different words: there are excellent reasons to probe fundamental forces at much higher energies – but also to go from accuracy to precision at lower energies with different tools. It seems to me that we are still at the beginning of this latter road.
1. HISTORY OF CP VIOLATION & PREVIEW OF THE FUTURE
It is possible that we live on one of many, many universes (or multi-verses). However our one is very special not only about the huge asymmetry of matter vs. anti-matter. The data tell us that baryonic (or known) matter produces around ~ 4.5%, dark matter ~ 26.5 % and vacuum (or dark) energy ~ 69 % in our universe. Those ratios are not very close zero or 100% as you might guess, but sizable; therefore we have to deal with surprizing landscape. Furthermore we have candidates for dark matter (like several versions of Super-Symmetry (=SUSY)). On the other hand we have hardly ‘realistic’ candidates for dark energy; at least I am too old to spend daytime to think about vacuum energy.
There is excellent evidence about the asymmetry of matter vs. anti-matter – namely ‘our existence’ on our earth. It was a real surprise to find that parity P and charge conjugation C are broken in charged weak forces. Our community quickly recovered that ‘τ ’ and ‘θ’ – called then – are the same state: K± mesons decay to both parity even and odd final states. Furthermore we have neutral ones –
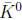 and K0 – producing two mesons that are differentiated by their lifetimes: KS and KL. Therefore KL was seen as parity odd mesons. Not only P & C violations were found, but also in maximal ways, namely charged weak mesons coupling only to left-chiral quarks. Also νL &
and K0 – producing two mesons that are differentiated by their lifetimes: KS and KL. Therefore KL was seen as parity odd mesons. Not only P & C violations were found, but also in maximal ways, namely charged weak mesons coupling only to left-chiral quarks. Also νL &
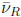 were found , but not νR &
were found , but not νR &
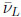 for massless neutrinos. It is fine in a simple realization of CPT invariance.
for massless neutrinos. It is fine in a simple realization of CPT invariance.
A true revolution happened in 1964: it was found that KL that usually decays into three pions, can also – rarely – to two pions 5. At first it was suggested to introduce non-linear terms into the Schrödinger equation with novel unobserved neutral particle U with KL → KS + U → π + U rather than giving up on CP symmetry. More data and more thinking showed we have found CPV in the data. Then Wolfenstein gave a paper about what is called super-weak CPV. In my view it is not even a model; it is a classification for models of CPV. In 1973 Kobayashi & Maskawa gave a published paper [1], where CPV can come from three classes: three (or more) families of quarks or/and charged Higgs states or/and more weak bosons with spin-one couplings to right-chiral bosons. At first some colleagues suggested the source of CPV comes from charged Higgs; afterwards we knew that we need (at least) three families of quarks for hadronic dynamics. Now we know that the CKM matrix produces at least the leading source of the measured CP asymmetries in the decays of kaons and B meson; that is a tested part of the SM.
No CPV has been established (yet) in the dynamics of charm hadrons, baryons in general (except our existence) and in the productions & decays of top quarks (before they can produce top hadrons [2]).
In the SM CP landscape is simple for leptons: when the three neutrinos are massless, one defines their leptonic flavor numbers by their couplings with charged leptons; furthermore e, µ and τ have not shown (yet) CP asymmetries in their decays – except in
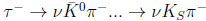 ... piggyback riding on
... piggyback riding on
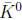 – K 0 oscillations [4].
– K 0 oscillations [4].
5 Actually Okun stated in his book ‘Weak Interactions of Elementary Particles’ published in 1963 in Russian - i.e., clearly before the discovery of CP violation (CPV) in 1964 - it is crucial to probe CP asymmetries.
Very short summary about past experience and prediction for the future:
(1) In the SM CP violation is not always tiny as we found out first in neutral kaons. In the transitions of B mesons they are large, even somewhat close to 100 % [3]. The SM produces at least the leading source for those, but our understanding of the impact of non-perturbative QCD still is limited quantitatively.
(2) CPV was found and established in neutral kaon decays, namely indirect and direct ones in ϵK and ϵ′/ϵK, respectively. However the ‘job’ has not been finished yet about fundamental dynamics. When one looks at the triangles from the CKM matrix, one seems the impact of our understanding of ϵK (like in Fig. 5 below). I was told there is ‘soon’ a chance that progress in lattice QCD will show the impact also on ϵ′.
(3) On the other hand the CKM dynamics has nothing to do with huge asymmetries in matter vs. anti-matter. Therefore we still have to think & work about this source.
(4) Measurable CP asymmetries need interferences of at least two amplitudes. Never mind that we have failed to understand matter vs. anti-matter in our universe. The interference can linearly depend on the amplitude of New Dynamics (ND) and thus allows with much more sensitivity.
(5) Asymmetric beams of e+e− collisions and new technologies for detectors with precision had entered a new era with the experiments BaBar at Stanford (U.S.A.), Belle at KEK (Japan) and now LHCb at CERN; it will continue with the experiment Belle-II at KEK. It is a real challenge to analyze huge amount of data. It is crucial to measure correlations between different final states – including multi-body FS in charm & beauty decays.
(6) On the theoretical side new tools with more accuracy probe fundamental dynamics including operator product expansion, heavy quark expansion and lattice QCD. While the source of CPV is weak forces, their impact depends on strong forces – i.e., nonperturbative QCD.
(7) Flavor independent CPV have been probed, in particular for EDMs in very different landscapes from elementary leptons to very complex states like nuclei or molecules – and we have to continue.
(8) Based on CPT invariance CPV & T are well connected. Of course one wants to probe CPT invariance. Usually it is assumed that EPR correlations are perfect.
(9) There are two classes of CP asymmetries:
(i) ‘Indirect’ CPV that can happen only on neutral mesons and need oscillations; these CP asymmetries depend on the time of decay; observables are defined by the initial final state (FS): K 0 (or KL), D 0, Bd & Bs6.
(ii) ‘Direct’ CPV can be seen in the decays of hadrons (and possibly also in some them in production connected with other states). Its impact depends on the FS and does not depend on the time of decay.
(iii) In neutral mesons one sees the interferences with both classes of CPV. Their impact depends on strong final state interaction (FSI) or re-scattering based on quantum theory amplitudes. It can be described in the worlds of hadrons or quarks.
(10) CPT invariance tells us that CPV is described by complex phases. However, it does not mean that all of these produce observables like about fermion fields and in particular about quark ones. One can change the phase of a quark field given CKM matrix element and rotate it away; it will re-appear in other matrix elements; for example:
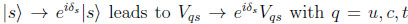 . Kobayashi & Maskawa showed we need three families of quarks to produce CPV and describe with a single complex phase [1] 7. In other words: one describes CPV in six triangles with very different patterns; however they give the same area. You might say that ‘maximal’ CPV means a phase is 90°. However such a statement is fallacious as said above.
. Kobayashi & Maskawa showed we need three families of quarks to produce CPV and describe with a single complex phase [1] 7. In other words: one describes CPV in six triangles with very different patterns; however they give the same area. You might say that ‘maximal’ CPV means a phase is 90°. However such a statement is fallacious as said above.
(11) Penguin diagrams are described in the world of quarks, gluons and weak bosons. Fig. (3) (a) sees Feynman diagrams with gluon & W gauge bosons and also b quarks in the initial state; part (b) describes wave lines for gauge bosons; it is assumed that non-perturbative QCD completes the FS. Sometimes art helps somewhere. There is a real challenge, namely to connect amplitudes in the world of quarks with those in the world of hadrons that are and can be measured.
6 Often the neutral B mesons are named Bd & Bs ; I prefer to use B = Bu,d,s,c to make it clearer.
7 CKM phase like the “Scarlet Pimpernel: Sometimes here, sometimes there, sometimes everywhere”.
This is a complex one on several levels. In the collisions of (anti-)baryons at low energies one hardly care about them being bound states of three constituent (anti-)quarks – unless one describes their EDMs, where one discusses the difference between current vs. constituent ones. When one talks about non-leptonic decays of hadrons, it is crucial to use current quarks. We know how to describe inclusive decays; however probing CPT violation the landscapes are much more complex, and we need more subtle tools to describe also multi-body FS. We cannot focus only on two-body FS.
There is a general comment: it is one thing to draw Feynman diagrams, but understanding the underlying forces is another thing; one needs more thinking and uses correlations with other transitions. One shows the impact of penguin diagrams in K → π decays, although loop diagrams are usually suppressed. On the other hand their impact is enhanced by chiral symmetry for two pions FS and somewhat for three pions. However this does not work for many-body FS in the decays of charm or beauty hadrons.
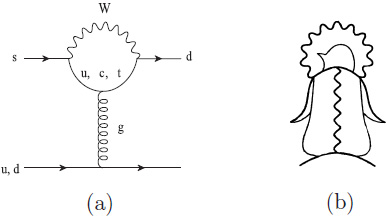 |
Fig. (3). (a) Diagrams of penguin amplitudes; the picture of the (b) diagram was reproduced from Parity by permission of T. Muta & T. Morozumi. |
(12) Usually one compares the predictions from models with the information gotten by fitting best the data. There is a good reason to say that the analyses are model insensitive. However it is only the first (and second) step; in particular when one has a good candidate for a real theory, one has to focus whether these predictions come around within two sigma or so and think & probe correlations with other data. Theoretical uncertainties are systemetic at best; often ‘predictions’ follow the fashion.
It shows the connection of CPV with the violation of T reversal (TV). One might say it is obvious in eiϕt to reach the same goal going down a different road. On the other hand, the landscape of T reversal is very complex. It depends on its definition. For example, we know that it happens already in classical physics: it is much easier to get ‘down’ than ‘up’ – i.e., the different scenarios of initial and final states. In this article I will discuss TV in fundamental forces.
(13) There is a short comment about ‘oscillations’ vs. ‘mixing’. Of course ‘mixing’ covers more items in dynamics than ‘oscillation’. However I see no reason to use the same word for different regions of dynamics.
· ‘Oscillations’ needs forces that can change the ‘flavor’ by two units. Their impact depends on the time of decay in well-know and measurable way. It depends on the initial neutral decaying hadrons like K 0 or Bd & Bs. Oscillation is a much more narrow meaning by focus on indirect CPV; oscillation is a crucial step to probe CPV, but it can happen without CPV – as we know so far about D 0 decays.
· I prefer to use the word of ‘mixing’ in narrow situations like s ↔ d about the Cabibbo angle or in general. It shows the connection of quarks with mass states that couple to weak charged bosons leading to the CKM matrix. Likewise for ‘massive’ neutrinos: they couple with charged leptons leading to the Pontecorvo–Maki–Nakagawa–Sakata matrix [5] (and maybe with Dark Matter).
2. CP ASYMMETRIES IN HADRONS’ DECAYS
CPV in neutral kaons and B mesons have been established; it depends on our quantitative understanding quark flavor dynamics including non-perturbative QCD. None have been found yet in charm hadrons; so far we have not enough rate to probe for top quarks [3].
One first focuses on the transitions of neutral mesons with richer landscapes. CPV was found in
 decays. We have many examples, and the future data will show more. We use tools based on quantum mechanics & quantum field theories and measure the correlations between different FS and differentiate the impact of ND and its features sometimes in subtle ways. It needs much more work & analysis. However I will emphasize the informations we get from many-body FS about direct CPV with accuracy and will discuss that about baryon and charged mesons decays below.
decays. We have many examples, and the future data will show more. We use tools based on quantum mechanics & quantum field theories and measure the correlations between different FS and differentiate the impact of ND and its features sometimes in subtle ways. It needs much more work & analysis. However I will emphasize the informations we get from many-body FS about direct CPV with accuracy and will discuss that about baryon and charged mesons decays below.
If ∆P ≠ 0 forces connect neutral flavor mesons P 0 (P0 = K 0, Bd, Bs, D0) and
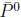
Therefore mass eigenstates described by linear amplitudes based on CPT [3].
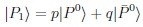 |
(3) |
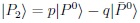 |
(4) |
are mass & width eigenstates with eigenvalues & their differences 8:
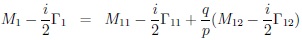 |
(5) |
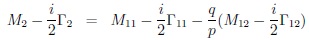 |
(6) |
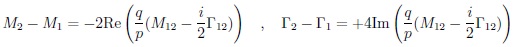 |
(7) |
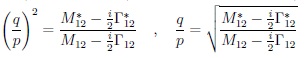 |
(8) |
q/p itself is not an observable. One can change the phase of anti-particles:
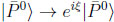 will modify the off-diagonal elements of M & Γ and thus q/p → e−iξ q/p. However both
will modify the off-diagonal elements of M & Γ and thus q/p → e−iξ q/p. However both
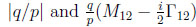 are invariant and observable in different ways:
are invariant and observable in different ways:
· P1 and P2 states in general are not orthogonal to each other:
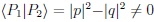 .
.
· This situation can be measured in semi-leptonic rates using CPT invariance with
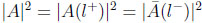 :
:
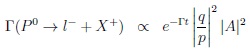 |
(9) |
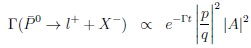 |
(10) |
One probes CPV based on
 oscillations, however it is independent of time:
oscillations, however it is independent of time:
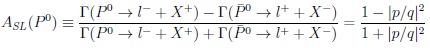 |
(11) |
8 There are opposite signs of q/p; using negative sign is equivalent to interchanging labels 1 ↔ 2.
It depends on the initial state with only indirect CPV with ∆P = 2, namely K0, Bd, Bs and D0 transitions.
· Basically quantum mechanics tell us about the two mass eigenstates P1 & P2 using the Schwartz inequality [3, 6] arrive at:
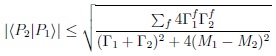 |
(12) |
This inequality is numerically relevant for kaons due to ΓL ˂ ΓS
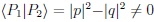 2ΔMK
2ΔMK
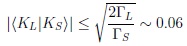 |
(13) |
as a very conservative bound: KL and KS are close to be odd and even CP states. Does it mean that we are just being lucky with 3mπ < MK < 4mπ or is a deep reason about these limits?
The landscape is more complex with non-leptonic decays about indirect and direct CPV even with
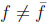 based on quantum field theories with CPT invariance [3]:
based on quantum field theories with CPT invariance [3]:
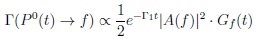 |
(14) |
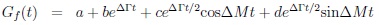 |
(15) |
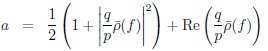 |
(16) |
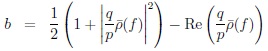 |
(17) |
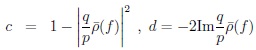 |
(18) |
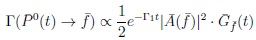 |
(19) |
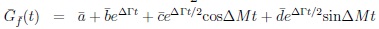 |
(20) |
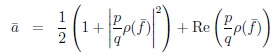 |
(21) |
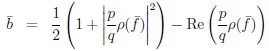 |
(22) |
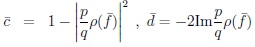 |
(23) |
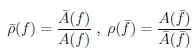 |
(24) |
It is important that
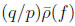 and
and
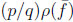 do not depend on the definition of the phases and therefore are observables, while (q/p) and
do not depend on the definition of the phases and therefore are observables, while (q/p) and
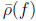 by itself are not.
by itself are not.
Here you can see the general situation. In our world we have |q/p| ~ 1 and ∆Γ/Γ ~ 0 (except for ∆Γ(KL)/(Γ(KL) + Γ(KS)), ∆Γ(KL)/Γ(KS) = 0.49). ∆Γ = 0 can happen only due to a miracle; however, ∆Γ can be smaller or larger than expected from SM values; the impact of ND can hide in the experimental and/or theoretical uncertainties.
When the FS are even/odd CP eigenstates, one gets:
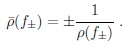 |
(25) |
For charged P mesons the landscapes look much simpler 9 – but not very much in reality:
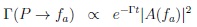 |
(26) |
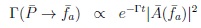 |
(27) |
There are several important statements, although they are not always obvious:
· Time depending rates show the impact of indirect vs. direct CPV in neutral mesons. The amplitudes of indirect ones depend in the initial states: K0, Bd, Bs and D0. These can be probed in two-body FS.
· Direct CPV affect differently FS in the decays of hadrons. It is not enough to understand the dynamics with two-body FS; it is crucial to measure three- and four-body FS with accuracy, but not only as a back-up information.
· The impact of strong re-scattering is crucial as discussed below. It happens in the world of hadrons (and of quarks) as indicated in fa vs.
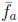 ; however it is a true challenge to describe them quantitatively with subtle theoretical tools.
; however it is a true challenge to describe them quantitatively with subtle theoretical tools.
3. THE LANDSCAPES OF K & B & D MESON DECAYS
3.1. Kaon Decays – First ‘Affair’
The existence CPV was first found in 1964 by KL → π+π− – i.e., the KL amplitude has a small non-zero CP odd component due to K0 −
 oscillations with ∆MK /ΓS = 0.49:
oscillations with ∆MK /ΓS = 0.49:
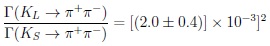 |
(28) |
The existence of this small rate is connected with the asymmetry in
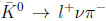 vs.
vs.
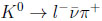 in the SM (and basically beyond) – i.e., indirect CPV:
in the SM (and basically beyond) – i.e., indirect CPV:
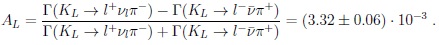 |
(29) |
While AL comes from oscillations, this asymmetry does not depend on the time of the decays. The scenarios of non-leptonic decays are more complex also for KL decays: weak forces produce KL → π+π−/π 0π 0, which are calibrated by KS decays:
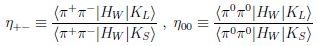 |
(30) |
We differentiate indirect vs. direct CPV:
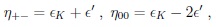 |
(31) |
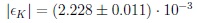 |
(32) |
The response from the theoretical community about CPV was slow. It was suggested by Wolfenstein that we have a ND, namely super-weak one with ϵ' = 0. However there was not a real theory, but a classification of theories for CPV.
3.2. New Standard Model ‘then’
Most HEP people ‘knew’ about three quarks, namely u, d, s; most thought of them as a mathemalical entities. Some outliers told about the fourth quark, namely c. To understand to underlying dynamics of CPV Kobayashi & Maskawa published a paper in 1973 that there are three classes of theories beyond the SM then, namely at least three families of quarks or right-handed charged currents or charged Higgs. Now we know that at least the leading source comes from three families with (u, d), (c, s) and (t, b) with weak forces SU(2)L × U (1).
We have to deal with somewhat different landscapes, namely we can probe data based on hadrons and predict transitions based on quantum field theories with quarks & spin-one weak bosons & gluons. This connection comes from the word of ‘duality’ in different levels; some are obvious, others are subtle.
For the SM one gets an unitary CKM matrix for three families with six charged quarks in pairs (u, d), (c, s) & (t, b):
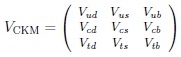 |
(33) |
It is described by six triangles. However one gets only four observables, namely three angles and one phase. Their patterns are quite different, but their have the same area. The general parameterization of flavor dynamics is not obvious.
3.2.1. Wolfenstein’s Original Parameterization & Refined Ones
Wolfenstein suggested a very good ‘usable’ one based on the expansion in the Cabibbo angle λ = sinθC = 0.223 with the three A, ρ and η being of the order of unity [8]:
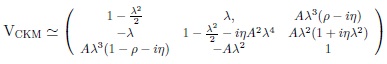 |
(34) |
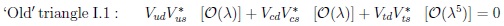 |
(35) |
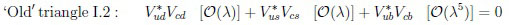 |
(36) |
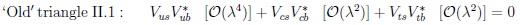 |
(37) |
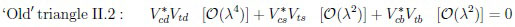 |
(38) |
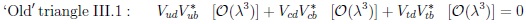 |
(39) |
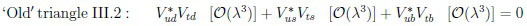 |
(40) |
The pattern is obvious, in particular about indirect CPV, namely very large in
 oscillations. It has been successful in describing the ‘golden’ triangle in Bd,u decays in Fig. (4), where triangle III.1 shows that the sizes of the three angles are quite similar. The angles φ1, φ2, φ3 are opposite the sides with
oscillations. It has been successful in describing the ‘golden’ triangle in Bd,u decays in Fig. (4), where triangle III.1 shows that the sizes of the three angles are quite similar. The angles φ1, φ2, φ3 are opposite the sides with
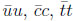 ; other people name angles β, α, γ.
; other people name angles β, α, γ.
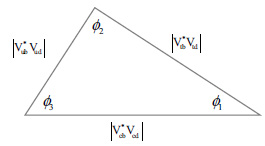 |
Fig. (4). The ‘golden’ CKM unitarity triangle. |
It is crucial to probe the correlations in the triangles. Fig. (5) shows that large CPV in Bd → ψKS is connected with very small one in KL → π transitions and the ratio of
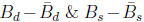 oscillations due to ∆MBd/∆MBs ; i.e., those observables (mostly) come from three triangles.
oscillations due to ∆MBd/∆MBs ; i.e., those observables (mostly) come from three triangles.
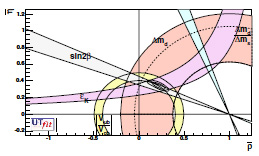 |
Fig. (5). The ‘golden’ CKM unitarity triangle fitted including the impacts from ϵK and ΔMBs from two other triangles. |
That successful description still has some weak points. There are some ‘tensions’ about the data and the expected predictions. Furthermore measured decays of Bd,u mesons give us η = 0.34 and ρ = 0.13, which are not close to unity. With three families of quarks one gets six triangles to decays of kaons, charm & beauty decays and top quarks. Four of those six ones one can probe directly. The patterns of these triangles are very different.
The SM produces at least the leading source of CPV in KL → 2π and B decays with good accuracy. Searching for ND we need even precision and to measure the correlations with other FS’s. The landscape of the CKM matrix is more subtle as pointed out [9].
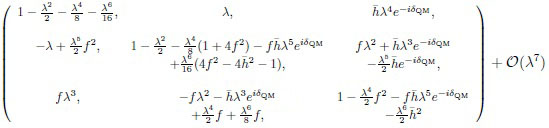 |
(41) |
with
 = 1.35, f = 0.75 & δQM ~ 90° and only expansion in λ = 0.223.
= 1.35, f = 0.75 & δQM ~ 90° and only expansion in λ = 0.223.
The ‘shapes’ of six triangles are different in subtle ways:
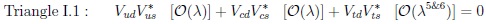 |
(42) |
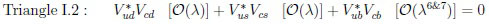 |
(43) |
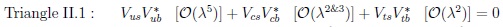 |
(44) |
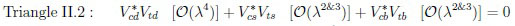 |
(45) |
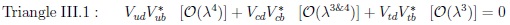 |
(46) |
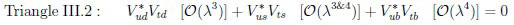 |
(47) |
The pattern in flavour dynamics is less obvious for CPV in hadron decays as stated before [10]; the situation has changed: we have to measure the correlations between four triangles, not focus only on the ‘golden triangle’. Some of the important points are emphasized:
· We have to probe triangle III.1 with precision in Bd,u transitions.
· Triangle II.1 has sizable impact on Bs amplitudes and connect with other Bd,u
decays.
· Triangle I.2 produces CP asymmetries in Singly Cabibbo Supressed (SCS) D decays, but hardly in Doubly Cabibbo Supressed (DCS) ones.
· Triangle I.1 can be probed in tiny
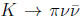 decays with small theoretical uncertainties.
decays with small theoretical uncertainties.
· Again: one has to focus on correlations with several triangles with accuracy 10.
3.3. Kaon Decays – Second ‘Affair’
The measured values of |ϵK| gives small experimental uncertainty; the challenge is to connect with the CKM parameters as shown in Fig. (5), namely mostly the impact of triangle I.1 on the golden one in triangle III.1.
Direct CPV is expressed through the ratio:
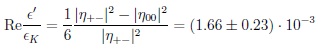 |
(48) |
These values do not do justice to the experimental achievement. The achievement becomes more transparent [3]:
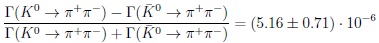 |
(49) |
There is no surprise that Re(ϵ' / ϵK) is small with the large top quark mass including the impact of penguin diagrams, (see Fig. 3). However the experimental uncertainty is sizable, and now Re(ϵ'/ϵK) gives no constraint on CKM parameters. More data and refined analyses of K → πγ & K → πγ allow deeper probes of chiral symmetry and in general better treatment of long-distance dynamics. It gives tests of LQCD as a subtle tool. Furthermore the LQCD community might be able to show that Re(ϵ'/ϵK) gives sizable (& novel) impact on the correlations with the golden triangle [11].
3.4. Future of Very Rare Kaon Decays
There is still an important point about understanding fundamental dynamics, namely to measure the rates of
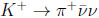 vs.
vs.
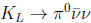
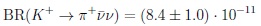 |
(50) |
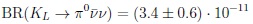 |
(51) |
3.5. CP Asymmetry in the Decays of Charged Mesons & Baryons
While ‘only’ direct CPV can effect the decays of baryons and charged mesons, one might think that the landscape is less complex. The opposite is (mostly) true:
(i) Direct CPV depend on FS and on the classes of decaying hadrons.
(ii) CP asymmetries do not depend on the times of the decays. Measuring time depending asymmetries is a very powerful tool.
(iii) One has to focus even more importantly on regional CPV where one needs at least three pseudo-scalar ones in the FS. As discussed below large ones have been found in B±.
3.6. Effective Transition Amplitudes
Strong re-scatterings happen all the time. Can we describe them quantitatively? Our control of non-perturbative QCD is limited so far. However it helps to deal with this challenge with tools following constraints coming from symmetries (broken or not). It has large impact on direct CP asymmetries with CPT invariance as discussed in Refs. [13-15]; it is given in Sect. 4.10 of Ref.[3] with much more details:
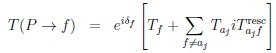 |
(52) |
 |
(53) |
where amplitudes Tajfresc describe FSI between f and intermediate on-shell states aj that connect with this FS. Thus one gets regional CP asymmetries:
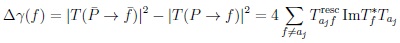 |
(54) |
CP asymmetries have to vanish upon summing over all such states f using CPT invariance between subclasses of partial widths:
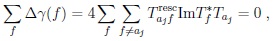 |
(55) |
These Eqs. (52,53) apply to amplitudes in general, whether for hadrons or quarks or
 boundstates in between 11. In which way one can connect the landscapes in hadronic and quark amplitudes – it depends. In the world of quarks one can describe them by refined tree, penguin etc. diagrams. Those give weak phases. Furthermore penguin diagrams coming from non-local operators produce ∆Γ for Bs,d mesons and somewhat for D0 one. Those give also imaginary part that one needs for FSI – however the situations are very ‘complex’ there. The ‘roads’ are quite different depending on the FS.
boundstates in between 11. In which way one can connect the landscapes in hadronic and quark amplitudes – it depends. In the world of quarks one can describe them by refined tree, penguin etc. diagrams. Those give weak phases. Furthermore penguin diagrams coming from non-local operators produce ∆Γ for Bs,d mesons and somewhat for D0 one. Those give also imaginary part that one needs for FSI – however the situations are very ‘complex’ there. The ‘roads’ are quite different depending on the FS.
3.7. Impact of Non-Perturbative QCD
The scenarios of the weak decays of beauty and charm hadrons are more complex than in kaon ones. There are several reasons:
· Two-body FS produce only small parts of CKM suppressed of D(s) decays and tiny in B(s) ones. There is no reason why two-body FS give us all the information that we need to understand dynamics and even less for only charged two-body ones.
· The worlds of hadrons and quarks are different. One can hide that by using ‘constitute’ quarks, which works fine for spectroscopy (in particular for strange hadrons), but not for weak forces. ‘Current’ quarks are based on theories, not just models. However they are connected in subtle ways, and we have to apply refined tools.
· In the world of quarks one can describe inclusive FS in beauty & charm hadrons, where we have to use ‘duality’ often in subtle ways. CPT invariance produces strong constraints. To connect finite data of hadrons with quarks descriptions one has to use tools based on chiral symmetry, broken U-spin symmetry, dispersion relations [16] etc. and insist on correlations with other transitions.
· Probing CPV in many-body FS one measures first averaged one and then regional ones with accuracies. It is not a good idea to just follow the best fits; it is much more important to understand the landscapes and their informations given to us. Of course the analysis has to be very acceptable – but not giving the best fits. Judgment helps significantly how to define regional asymmetries.
· One measures three-body FS for several reasons with a long history [17]. We know how to probe Dalitz plots including regional ‘morphologies’; it has been emphasized not only use ‘fractional’ asymmetries, but also about different tools [18] and compare their results. In my view it is not the final step; we have to use more sutble theoretical tools like dispersion relations that depend also on data about low energy collisions of hadrons [16] – and some judgment.
The landscapes are very different already qualitatively between ∆B ≠ 0 and ∆C ≠ 0.
3.7.1. Case I: Broken U-Spin Symmetry
With quarks one describes mostly inclusive transitions. ‘Current’ quarks with mu < md < ms are based on theory. I-, U- & V-spin symmetries deal with u ↔ d, d ↔ s & u ↔ s. These three symmetries are obviously broken on different levels, and these violations are connected in the SM. The operators producing inclusive FS depend on their CKM parameters and the current quark masses involved there. However the real scale for inclusive decays is given by the impact of QCD, namely
 ~ 1 GeV as discussed many times.12 Thus the violations of U- & V-spin symmetries are small, and tiny for I-spin one. We can deal with inclusive rates and asymmetries of beauty and maybe charm hadrons using effective operators in the world of quarks.
~ 1 GeV as discussed many times.12 Thus the violations of U- & V-spin symmetries are small, and tiny for I-spin one. We can deal with inclusive rates and asymmetries of beauty and maybe charm hadrons using effective operators in the world of quarks.
The connections of inclusive with exclusive hadronic rates are not obvious at least, in particular about quantitative ways. The violations of I-, U-(& V-)spin symmetries in the measurable world of hadrons are expected to scale by the differences in pion and kaon masses, which are not small compared to
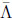 (or [mK2-mπ2]/[mK2+mπ2]). This is even more crucial about direct CPV and the impact of strong re-scattering on amplitudes.
(or [mK2-mπ2]/[mK2+mπ2]). This is even more crucial about direct CPV and the impact of strong re-scattering on amplitudes.
Going back to the history: Lipkin had suggested that U-spin violations in B decays are of the order of 10 % [19] in CKM favored ones. They might be larger in suppressed ones. The worlds of hadrons (or ‘constitute’ quarks) are controlled by FSI due to non-perturbative QCD; they show the stronger impact on exclusive ones. For good reasons it has been stated that violation of U-spin symmetry is around O(10%) in inclusive decays. It can be seen in the sum of exclusive ones in large ratios that go up and down much more sizably. The papers [20] suggest one can probe U-spin symmetry with three-body FS with small theoretical uncertainties and even with only charged hadrons in the FS; I quite disagree on both, see [10, 21, 22] with more comments & details: ‘Effective transition amplitudes’ or re-scattering as discussed above (see Sect. 3.6) produce large impact. I suggest to think about the informations gotten from Sect. 3.8.2 using CPT invariance about their subtle morphologies discussed below.
3.7.2. Case II: Impact of Penguin Operators vs. Diagrams
Penguin diagrams (Fig. 3) were introduced for kaon decays where is little differences between exclusive vs. inclusive decays. The impact of penguin operators in CKM suppressed decays of beauty hadrons are enhanced by chiral symmetry in their amplitudes, in particular for two body FS with pions and somewhat for kaons. However in charm hadron transitions the leading source of penguin diagrams is not given by local or even short-distance dynamics.
3.8. Bu,d,s Decays
The SM gives at least the leading source of CP asymmetries in B transitions [with the still possible exception in Bs → ψφ, ψf0(980) ones]. Now we are probing for impact of ND in CP asymmetries and its features.
3.8.1. Indirect CPV in
 Oscillations
Oscillations
Using ∆ΓBd < ∆MBd ~ Γ Bd as expected due to the large top quark mass, one states:
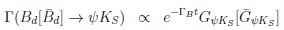 |
(56) |
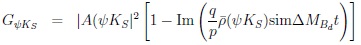 |
(57) |
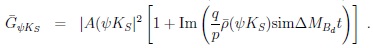 |
(58) |
CPV is described by Im
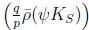 . One first needs ∆MBd ≠ 0 to measure this asymmetry, which depends on the time of decay. In other words:
. One first needs ∆MBd ≠ 0 to measure this asymmetry, which depends on the time of decay. In other words:
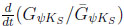 ≠ 0 actually in a special way: sin∆MBd t shows the connection with ‘odd’ T symmetry 13:
≠ 0 actually in a special way: sin∆MBd t shows the connection with ‘odd’ T symmetry 13:
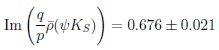 |
(59) |
In the SM for the ‘golden’ triangle one gets Im
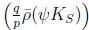 = sin2φ1[β].
= sin2φ1[β].
Refined parameterization of the CKM matrix show that the maximal value possible in the SM is ~ 0.72 [10], not really close to unity due to correlations with other transitions.
The situation is different about
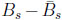 oscillations with ∆MBs = 26.9 and ys ~ 0.07: very fast oscillation has been established, but no CPV has been found (yet):
oscillations with ∆MBs = 26.9 and ys ~ 0.07: very fast oscillation has been established, but no CPV has been found (yet):
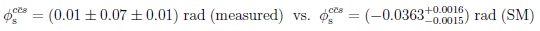 |
(60) |
These data are close to SM values, but also consistent with ND’s sizable contributions – even leading source there – or with the opposite sign. It is interesting that recent LHCb data about Bs → ψπ+π- => ψf (980) see no obvious contribution from scalar σ => π+π-.
3.8.2. Direct CPV in B Decays
The situations of decays of Bu,d,s (and even BC) are complex (for optimistic physicists); they are ‘rich’ where one can find the impact of ND or at least important lessons about non-perturbative forces from QCD. Again first one focus on (quasi-)two-body FS about sizable asymmetries in B+ → DCP+K+, which has impact of measuring the angle φ3/γ. Furthermore penguin diagrams contribute to CPV in Bd → K+π-, K*(892)+π-, Bs → π+K- and B+ → ηK+ on different levels 14. The real challenge is to establish the impact of ND as a non-leading source. In the world of quarks one can show the ways to connect with hadronic FS with penguin diagrams due ‘duality’, which is a true challenge in a quantitative way.
Probing CPV in the SM suppressed decays one gets only a number in two-body FS. To connect the information we get from the data with the fundamental dynamics is not trival – but it is not enough about forces: we have to probe three- & four-body FS etc. We describe three-body FS due to two-dimensional Dalitz plots. The first step is to measure averaged CPV which also give numbers, but still connected with two-body ones. However it is crucial to probe regional asymmetries. I give recent examples about the power and the tools including CPT invariance.
3.8.3. CP Asymmetries in B± Decays
In this article I focus on charged three-body FS, although I will talk also about the general landscape including CPT. LHCb data give small rates for CKM suppressed B+ decays to charged three-body FS, which are not unusual:
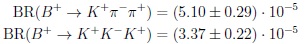 |
(61) |
LHCb data also show sizable CP asymmetries averaged over the FS [23]:
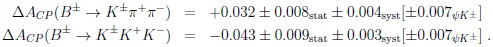 |
(62) |
It is very interesting that these CP asymmetries come with opposite signs due to the road to CPT invariance and give us lessons about underlying dynamics. Still it is not surprising. Furthermore they show ‘regional’ CP asymmetries defined by the LHCb collaboration:
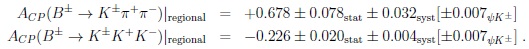 |
(63) |
One expects that ‘regional’ asymmetries are larger than averaged ones. At least they show the impact of re-scattering. Again, one sees the opposite signs; however the sizes are quite different. Furthermore one has to remember that scalar resonances (like f0(500)/σ & κ) produce broad ones that are not described by Breit-Wigner parametrization; instead they can be described by dispersion relations [16] in details (or other ways). At the qualitative level one should not be surprised. Probing the topologies of Dalitz plots with accuracy one might find the existence of ND. Most of the data come along the frontiers. However, the centers are not empty; as we know direct CP asymmetries need interferences between (at least) two amplitudes, and the impacts of resonances are different for narrow vs. broad ones. We need more data, but also deeper thinking about underlying dynamics, whether those give us new lessons about non-perturbative QCD – or also about ND.
One looks at even more CKM suppressed three-body FS:
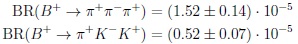 |
(64) |
It is not surprising that these rates are smaller than those in Eq.(61). LHCb has measured these averaged CP asymmetries [24]:
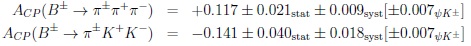 |
(65) |
As I have said above, re-scattering happen, although we have so far little quantitative control. Again, it is interesting that they come with opposite signs with only charged FS mesons like above in Eq. (62), but they seems to be sizably larger than those. Maybe it is not ‘luck’, but a pattern. On the other hand, it is not an obvious symmetry, but it depends on the situations. Penguin diagrams are suppressed, but they can produce large weak phases b → “W-(t, c, u)” → d. It is a true challenge to understand its impact.
LHCb has shown for ‘regional’ CP asymmetries [24]:
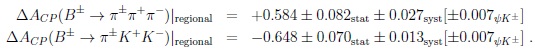 |
(66) |
Again it is not surprising that these asymmetries come with opposite signs. Maybe it might be somewhat surprising that the impact on regional asymmetries are so large. We need more data, find other regional asymmetries and work on correlations with other FS. Importantly we need more thinking to understand what the data tell us about the underlying dynamics including non-perturbative QCD. Actually we have tested tools like dispersion relations & chiral symmetry; however we have to apply them with more precision It seems that the landscapes are more complex as said before and shows the impacts of broad resonances.
3.9. T Violation With & Without EPR Correlations
Once one has established CPV directly, one has found T violation indirectly with CPT invariance. However the situation is more subtle due to EPR correlation; actually it is a ‘blessing in disguise’. People are not fans of history prefer the name of ‘entanglement’ 15. For a special situation one has a pair of neutral B mesons who are produce in single coherent quantum state with spin-one & C odd where their oscillations are highly correlated with each other as done at BaBar & Belle experiments:
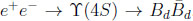 . This pair cannot transmogrify itself into a
. This pair cannot transmogrify itself into a
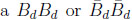 . To say it in different ways. Using the neutral mass eigenstates B1 & B2 one gets only e+e- → ϒ(4S) → B1B2, but not FS with B1B1 or B2B2. The simplest and best measured asymmetry gives ϒ(4S) → (l-X )B (ψKS)B vs.
. To say it in different ways. Using the neutral mass eigenstates B1 & B2 one gets only e+e- → ϒ(4S) → B1B2, but not FS with B1B1 or B2B2. The simplest and best measured asymmetry gives ϒ(4S) → (l-X )B (ψKS)B vs.
ϒ(4S) → (l+
 )B (ψKS)B vs ϒ(4S) → (l-
)B (ψKS)B vs ϒ(4S) → (l-
 )B (ψKS)B in the asymmetry of e+e- collisions. One can measure the differences in the semi-leptonic & non-leptonic decays. Those depend on ∆t, but also very consistent with sin[∆MBd ∆t] as expected. However there is more information, namely ∆t = 0 within the experimental uncertainties. One has assumed CPT only for semi-leptonic decays, not non-leptonic one, as pointed out last century, shown on the Fig. (6). The landscape of CPT violation has been probed with more details in Ref. [25] – but still assumes perfect EPR correlations.
)B (ψKS)B in the asymmetry of e+e- collisions. One can measure the differences in the semi-leptonic & non-leptonic decays. Those depend on ∆t, but also very consistent with sin[∆MBd ∆t] as expected. However there is more information, namely ∆t = 0 within the experimental uncertainties. One has assumed CPT only for semi-leptonic decays, not non-leptonic one, as pointed out last century, shown on the Fig. (6). The landscape of CPT violation has been probed with more details in Ref. [25] – but still assumes perfect EPR correlations.
3.10. Weak Decays of Charm Mesons & Baryons
No CP asymmetry has been found in charm mesons or baryons. On the other hand we have learnt that the landscape of charm transitions is complex in different directions. One is obvious, namely one can probe SCS & DCS ones, where the SM gives small weak phases of O(0.001) in the first and basically zero on the latter. The second one is not so obvious: even when they depend on the same weak phase, they can be affected by (strong) re-scattering in different ways like two-, three- & four-body FS. A well-known example: Γ(D0 → K+K-)/Γ(D0 → π+π-) ~ 3, while Γ(D0 → K+K-π+π-)/Γ(D0 → 2π+2π-) ~ 1/3. There are other examples with D0 → π+π- & D0 → K+K-π0, KS K-π+, KS K+π-.
3.10.1. Indirect CPV in
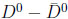 Oscillation
Oscillation
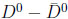 oscillations have been established by the data with
oscillations have been established by the data with
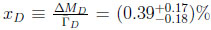 and
and
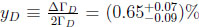 . The amplitude is described by SCS transitions, but also with the interference between Cabibbo favored & DCS ones. The impact of ND can be seen mostly in xD due to local operators; the situation about yD is more complex [26].
. The amplitude is described by SCS transitions, but also with the interference between Cabibbo favored & DCS ones. The impact of ND can be seen mostly in xD due to local operators; the situation about yD is more complex [26].
3.10.2. Direct CPV in SCS Decays of Mesons
In the world of hadrons strong re-scattering connect
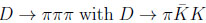 and back. For very good reasons one describes three-body FS with amplitues with quasi-two body FS and their interferences; however scalar resonances often are described by broad ones where one cannot use Blatt-Wigner parametrization. Furthermore the Dalitz plots are not empty; therefore interferences happens at many locations. The SM is expected to produce averaged values for SCS decays O(0.001) and larger values for regional asymmetries. The questions are: how much, where and about the impact of CPT invariance on subclasses with only charged hadrons or not. One has to probe averaged & regional ones in Ds± → K±K+K-, K±π+π- and to think about correlations with D± decays.
and back. For very good reasons one describes three-body FS with amplitues with quasi-two body FS and their interferences; however scalar resonances often are described by broad ones where one cannot use Blatt-Wigner parametrization. Furthermore the Dalitz plots are not empty; therefore interferences happens at many locations. The SM is expected to produce averaged values for SCS decays O(0.001) and larger values for regional asymmetries. The questions are: how much, where and about the impact of CPT invariance on subclasses with only charged hadrons or not. One has to probe averaged & regional ones in Ds± → K±K+K-, K±π+π- and to think about correlations with D± decays.
Chiral symmetry is a very good tool for 3π FS; however the power of that is decreased for FS with Kπ,
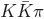 and 3K. Again – how much?
and 3K. Again – how much?
3.10.3. Basically Zero CP Asymmetries in DCS Decays
The refined parameterization of the CKM matrix [9] gives basically zero direct CPV in DCS in D± → K±π+π-/K±K+K- and in exotic decay Ds± → K±K±π±. The first step is to establish averaged CPV in D(s) decays, then the second one is to probe regional ones. Again it needs some judgment to define regional asymmetries with finite data. While the rates are very small, there is no ‘background’ from the SM. Furthermore the ‘exotic’ Ds decays should be more standing out due to ∆S = 2 in the FS; at least they give us unusual lesson about QCD.
I add a comment about CP asymmetries in the decays of charm baryons like Λc+ . One can compare favored decays Λc+ → pK-π+ with DCS Λc+ → pK+π-:
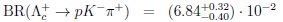 |
(67) |
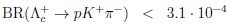 |
(68) |
The favored decay has been established. For the future it should be transformed from “accuracy” to “precision”. The latter one has not been founded yet; the first step is to establish with some accuracy. The second step would be to probe CPV in Λc+ → pK+π- as calibrated by Λc+ → pK-π+, where there is hardly a chance to find CPV in general. It would be an excellent achievement to find CPV due to two points: to establish CPV in baryon decays for the first time – and also to find impact of ND at the same time without background from the SM. Then the third step would be to probe regional CP asymmetries.
4. INTERMEZZO - ELECTRIC DIPOLE MOMENT (EDM)
It is a rich landscape that shows the connection of HEP, Hadrodynamics, nuclear, atomic & molecule physics.
· We have found large CPV flavor dynamics, but it has nothing to do with the truly huge observed asymmetry in known matter vs. anti-matter of baryons.
· EDMs have been probed in many different situations [27], but none has been found yet despite hard work both on the experimental & theoretical side. Still I see no good reason to give up: future work might tell us the direction for the dynamics to produce that asymmetry.
· QCD faces the challenge to solve the problem with basically zero contributions of the operator
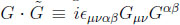 and the gateway for ‘traditional’ and ‘novel’ axions.
and the gateway for ‘traditional’ and ‘novel’ axions.
· There might be a connection of known vs. dark matter.
· A very general statement: to understand fundamental dynamics it needs a lot of time, new tools – and thinking & new ideas.
Direct test of T invariance comes for single particle static transitions. The energy shift of a system due to external small electric field can be described in powers of
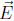 :
:
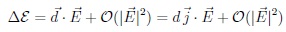 |
(69) |
The linear vector di is called the EDM. A non-zero value of di show the violation both discrete P and T symmetries. The crucial point is not ‘elementary’, but ‘non-degeneracy’ of the impact of the dynamics. It is a well-known example to compare the neutron dN with water molecules or ‘dumb-bells’ based on classical forces [3].
In quantum field theory EDMs are described by an operator in the Lagrangian:
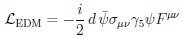 |
(70) |
In the SM one gets EDM values for neutrons, deuterons, molecules and also for e, µ & τ ones that are clearly beyond what one can reach. Therefore it is a rich landscape for the existence of ND and its features, if you are patient enough to make the efforts that are needed with thinking about & working on ideas.
The situation is more subtle: QCD can produce CPV in flavor independent transitions, namely EDMs in hadrons. It was realized long time ago that QCD with vector bosons have a problem used ‘U (1)A problem’ [3]. Let us look at QCD with only one family with u & d quarks. With massless quarks – which is very close to
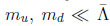 – one might think that QCD possesses a global U (2)L × U (2)R symmetry. Indeed the vectorial component U (2)L+R is conserved even after QM corrections and axial SU (2)L-R also in subtle ways to give masses to Wµ± and Z0. However about U (1)L-R? Axial currents are conserved in the classical symmetry due to chiral invariance for massless quarks; however they are not conserved called ‘quantum anomaly’ (or ‘triangle anomaly’) due to one-loop corrections with internal quarks:
– one might think that QCD possesses a global U (2)L × U (2)R symmetry. Indeed the vectorial component U (2)L+R is conserved even after QM corrections and axial SU (2)L-R also in subtle ways to give masses to Wµ± and Z0. However about U (1)L-R? Axial currents are conserved in the classical symmetry due to chiral invariance for massless quarks; however they are not conserved called ‘quantum anomaly’ (or ‘triangle anomaly’) due to one-loop corrections with internal quarks:
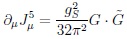 |
(71) |
The resolution of the U (1)L-R due to complex structure of the QCD ‘vacuum’ comes with a price, namely the ‘Strong CP Problem’. The U (1)L-R & Strong CP is actually intertwined, when one includes the weak dynamics 16:
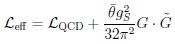 |
(72) |
with the observable
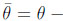 arg detM. It describes the mixing matrix of U=(t,c,u) and D=(b,s,d) quarks. Photon can couple neutrons with internal virtual protons & pions. One of the two effective pion nucleon operators couple by ordinary QCD, while to other one are due
arg detM. It describes the mixing matrix of U=(t,c,u) and D=(b,s,d) quarks. Photon can couple neutrons with internal virtual protons & pions. One of the two effective pion nucleon operators couple by ordinary QCD, while to other one are due
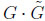 . A guess tells us:
. A guess tells us:
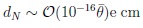 |
(73) |
The limit from the data gives:
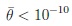 |
(74) |
While it is possible or worse ‘accidentally’, but very ‘un-natural’.
4.1. Traditional & Novel Axion Scenarios
Most members of our community agree that one needs organizing principle to produce the required cancellations. The best known tool is some kind of symmetry. A real intriguing ansatz is to assume that a physical quantity usually used as a constant is re-interpret as a dynamics degree of freedom. In this case it was suggested by Peccei & Quinn [28], namely to add the SM a global U (1)PQ as a Nambu-Goldstone boson which is axial with following properties:
· it is a classical symmetry;
· it is subject to an axial anomaly;
· it is broken spontaneously as well and
· possesses a huge vacuum expectation value (VEV) υPQ > υEW.
Previously we thought there are two classes, namely (A) ‘visible’ axion with ma ~ O(1 MeV), and (B) ‘invisible’ axion with ma < 1 MeV. It seems there is no chance that class (A) axion can exist. ‘Invisible’ axion might be found using coupling of axion with two photons. The name ‘invisible’ is obvious, namely due to the tiny axion mass the lifetime is larger than the age of our universe, and couplings to other fields are so minute that they would not betray their presence under ‘ordinary’ circumstances. The best tool might be by conversion an axion into a photon in a strong magnetic field B [29]:
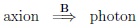 |
(75) |
It is still probed in our present world (including solar system due to astrophysical indirect information).
Later ‘old’ cosmology enters the ‘scene’: it gave lower bound on the mass:
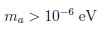 |
(76) |
Then connections of dark matter suggest stronger bounds:
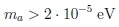 |
(77) |
Does it mean that the ‘dawn’ of axions goes to the ‘dusk’ ? Maybe the landscape of axion dynamics is even more subtle; namely actually PQ symmetry can be broken not only in QCD anomaly, but also in the UV region in many ways (and ideas) due to connection with gravity, gravitational waves, string theoretical realization of the QCD axion etc. Axions produced in the very early universe, can be part of the Dark Matter (and maybe also in Dark Energy) in the present universe and can be tested experimentally and directly. For example, it was described with more observables in the Refs. [30-32] about the PLANCK & BICEP2 data.
I am not convinced (yet) by some comments; however even if those projects will not be realized, they show the active situation in fundamental physics, which is wonderful in my view: a true ‘Renaissance’ gets from an excellent idea about the impact of symmetries.
5. PROBING CP ASYMMETRIES IN LEPTONIC TRANSITIONS
In the SM the landscape of CPV in hadrons and leptons are quite different. There the charged leptons and neutrinos are elementary with no original CPV. This century data showed us that neutrinos are not massless due to oscillations. Some of us think that CPV in neutrino oscillations can show the road to understand the huge difference between matter vs. antimatter. It also shows we need a very long time efforts to make progress there.
The SM landscape of leptonic dynamics about CPV is not very complex with massless neutrinos and e, µ and τ transitions. One can see it as not very interesting – or opposite, since there is hardly SM background on the theoretical side.
5.1. τ Cabibbo Suppressed Decays
Present data about CPV in SCS τ decays τ − → νKS (π...)− show one can compare SM prediction due to well-known
 oscillation with a difference of 2.9 sigma:
oscillation with a difference of 2.9 sigma:
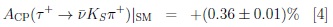 |
(78) |
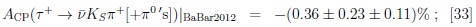 |
(79) |
one can note the sign. One can probe CPV decays like τ − → νK −π 0, νK−π+π−etc. and think about correlations due to CPT. We have to probe CPV in several FS like τ − → νK −π 0, νK −π+π−, νKS π−η.
Now available data probe only integrated CP asymmetries. It is important to probe regional CP asymmetries in τ − → ν [S = −1] FS; we have to wait for Belle II (and Super-Tau-Charm Factory if & when it exists). Furthermore one has to compare regional data from τ − → ν [S = 0] FS like τ − → ν π−π 0, ν π−η, ν π−π+π−, ν π−π 0π 0 etc. with accuracy. It is a test of experimental uncertainties; it would be a miracle to show CPV there.
It is important (as pointed out two years ago) to measure the correlations with D+ → K +π+π−/K +K +K − etc. [34]. Furthermore we have to look for regional asymmetries and spin correlations in the pairs of τ +τ −, in particular with polarized e+e− beams if we can use them.
5.2. CPV in Neutrino Oscillations
PMNS matrix very different than CKM matrix already in qualitative ways. In the world of quarks and also charged leptons masses they follow the catholic hierarchy. The situation is quite different about neutrino masses and angles. Furthermore neutrinos might have be partly Majoran. In general the three angles of the PMNS matrix [5] differ sizably from zero.
It is a very long time project to probe CPV in neutrino oscillations, which are affected by the environment of very mostly baryons rather than anti-baryons.
SUMMARY AND ABOUT THE FUTURE
Now we have entered the era where ‘accuracy’ has been changed into ‘precision’ with better tools including much better understanding of strong forces – and the possible connection with dark matter.
Up to now CPV basically have been measured in two-body FS in kaons and B mesons. It is crucial to probe many-body FS in kaons, Du,d,s and Bu,d,s and in baryons in general. Furthermore we have to use CPT as a tool to connect informations from different FS and regional CPV. EDMs in nuclei & molecules show us a new road for ND even, when it is not connected with the asymmetry in matter vs. anti-matter.
No CPV or TV has been found in leptonic dynamics with small limits so far. However we have to continue with precision, not only to understand those, but have a chance to find the source of the huge asymmetry in baryons vs. anti-baryons. Finally we know that the SM is not enough in our universe due to dark matter existence & neutrino oscillations. Therefore we have to probe CPV in neutrino oscillations, although it is a true challenge where we need long time projects based on HEP, Hadrodynamics & Nuclear Physics and combine their informations.
NOTES
1 ‘Cause’ = symmetry, yet ‘army’ = data.
2 Not all colleagues are so polite to give such credit.
3 Often the word of ‘entanglement’ has been used in this situation.
4 “All animals are equal, but some animals are more equal than others!” G. Orwell, ‘Animal Farm’.
5 Actually Okun stated in his book ‘Weak Interactions of Elementary Particles’ published in 1963 in Russian - i.e., clearly before the discovery of CP violation (CPV) in 1964 - it is crucial to probe CP asymmetries.
6 Often the neutral B mesons are named Bd & Bs ; I prefer to use B = Bu,d,s,c to make it clearer.
7 CKM phase like the “Scarlet Pimpernel: Sometimes here, sometimes there, sometimes everywhere”.
8 There are opposite signs of q/p; using negative sign is equivalent to interchanging labels 1 ↔ 2.
9 One can easily connect the expressions given for P0 vs.
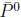 with ΔГ = 0 = ΔM.
with ΔГ = 0 = ΔM.
10 I see a connection of ‘correlations’ for a well-known joke: “In a circus an artist put tables & chairs together and jump to the top with a head-stand using broom-stick to produce balance - and play with a fiddle. One of the men watching that said to his wife: He is not like Haifetz.”
11 In principle one has to include baryons qiqjqk, but I will not discuss that in this article.
12 For good reasons one uses different and smaller ΛQCD ~ 0.1 – 0.3 GeV for describing jets in collisions.
13 To be precise: PDG2015 gives a value for B0 → J/ψ(nS) K0; I ignore direct CPV in those FS, while PDG2015 gives C(B0 → J/ψ(nS)K0) = (0.5 ± 2.0)·10-2.
14 Here one has also interference with indirect CPV in Bd → π+π-.
15 ‘Entanglemant’ seems to push out `EPR correlations' more and more recently in the literature; for me it is not only unfair, but worse
by ignoring the history of quantum mechanics; furthermore it ignores to establish large CP asymmetries in e+e-
→ Bd
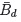 .
.
16 Often our community is sloppy with the names understanding the connections; other examples below: KSVZ or DFSZ axion.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This work was supported by the NSF under the grant numbers PHY-1215979 and PHY-1520966.
REFERENCES
| [1] | Kobayashi M, Maskawa T. CP Violation in the Renormalizable Theory of Weak Interaction Prog Theor Phys 1973; 49: 652-7. |
| [2] | Bigi II, et al. Phys Lett B 1986; 181: 157. |
| [3] | Bigi II, Sanda AI. CP Violation, 2nd ed. In: Cambridge Monographs on Particle Physics, Nuclear Physics and Cosmology. Cambridge University Press 2009. |
| [4] | Bigi II, Sanda AI. Phys Lett 2012; B625: 47-52.; Grossman Y, Nir Y. JHEP 2012; 1204: 002. |
| [5] | Pontecorvo B. JExpTheorPhys 1957; 33: 549.; Maki Z, Nakagawa M, Sakata S. Prog Theor Phys 1963; 30: 727. |
| [6] | Bell JS, Steinberger J. Proc 1965 Oxford Int Conf on Elementary Particles, Rutherford High Energy Lab, Didcot. |
| [7] | http://pdg.lbl.gov |
| [8] | Wolfenstein L. Phys Rev Lett 1983; 51: 1945. |
| [9] | Ahn YH, Cheng H-Y, Oh S. Phys Lett B 2011; 703: 571. arXiv: 1106.0935 |
| [10] | Bigi II. arXiv:1306.6014 [hep-ph], talk given at FPCP2013 Flavor Physics and CP Violation 2013. |
| [11] | Lehner Ch. talk given at the In: Workshop `Lattice Meets Continuum'; Siegen (Germany). 2014. |
| [12] | Buras AJ. arXiv: 15100028 [hep-ph] 2015. |
| [13] | Bigi II, Khoze VA, Uraltsev NG, Sanda AI. CP Violation. World Scientific 1988; pp. 175-248. |
| [14] | Uraltsev NG. Proceedings of DPF-92 http://arxiv.org/abs/hep-ph/9212233 1992. |
| [15] | Wolfenstein L. Final-state interactions and CP violation in weak decays. Phys Rev D Part Fields 1991; 43(1): 151-6. |
| [16] | Donoghue JF. hep-ph/9607351 ; Pennington MR. Proceedings of MESON2002, arXiv:hep-ph/0207220 2002.; Gardner S, Meissner U-G. PhysRev 2002; D 65: 094004. arXiv:hep-ph/0112281; Pelaez JR, Yndurain FJ. PhysRev 2005; D71: 074016. hep-ph/0411334; Pelaez JR, et al. Proceedings of the Hadron XIV International Conference on Hadron Spectroscopy. arXiv:1109.2392 |
| [17] | Golden M, Grinstein B. Phys Lett 1989; B222: 501-6.; Bigi II. Proceedings of Tau-Charm Factory Workshop, ConfProc. C890523: 169-95. |
| [18] | Bediaga I, et al. PhysRev 2009; D80: 096006. arXiv:0905.4233[hep-ph]; Bediaga I, et al. PhysRev 2012; D86: 036005. arXiv:1205.3036; Williams M, et al. PhysRev 2011; D84: 054015. |
| [19] | Lipkin H. Phys Lett B 2005; 621: 126. arXiv:hep-ph/0503022 |
| [20] | Lorier N R-L, Imbeault M, London D. PhysRev 2011; D84: 034040. arXiv:1011.4972 [hep-ph]; Bhattacharya B, Gronau M, Rosner J L. CP asymmetries in three-body B± decays to charged pions and kaons Phys Lett 2013; B726: 337. arXiv:1306.2625; He X-G, Li G-N, Xu D. PhysRev 2015; D 91: 014029. arXiv:1306.2625 |
| [21] | Bigi II. arXiv:150903899v2 [hep-ph] 2015. |
| [22] | Bigi II. Frontiers of Physics 2015 June; 10(3): 101203. arXiv:1503.07719 [hep-ph] |
| [23] | Aaij R, et al. LHCb collab. Phys Rev Lett 2013; 111: 101801. |
| [24] | Aaij R, et al. LHCb collab. Phys Rev Lett 2014; 112: 011801. |
| [25] | Lees J P, et al. Phys Rev Lett 2012; 109: 211801. arXiv:1207.5832 |
| [26] | Bianco S, et al. Cicerone for the physics of charm RivNuovoCim 2003; 26N7(Sect. 9.4): 1-200. arXiv:hep-ex/0309021 |
| [27] | Raidal M, et al. EurPhysPhysJ 2008; C57(in particular on Sect. 9): 13-182. arXiv:0801.1826 |
| [28] | Peccei R, Quinn H. Phys Rev Lett 1977; 38: 1440.Phys Rev 1977; D16: 1791. |
| [29] | Sikivie P. A pioneer about the `road': PhysRevLett 2014; 113(20): 201301.PhysLett 2011; B695(22)LectNotes Phys 2008; 741(19) arXiv:1409.2806; arXiv:1210.0040 arXiv:1003.2426 [astro-ph] astro-ph/0610440 |
| [30] | Choi K. Invited talk at COSMO In: Chicago 2014.; Choi K, Jeong KS, Seo M-S. JHEP 2014; 1407: 092. arXiv:1404.3880; Choi K, Kim H, Yun S. Phys Rev 2014; D90: 023545. arXiv:1404.6209 |
| [31] | Graham PW, Rajendram S. Phys Rev D Part Fields Gravit Cosmol 2013; 88: 035023. arXiv:1306.6088 |
| [32] | Kim JE. Nucl Phys B, Proceedings Suppl 2014. arXiv:1410.5045 [hep-ph] |
| [33] | PhysRev 2012; D85: 031102.Erratum-ibid 2012; D85: 099904. arXiv:1109.1527 [hep-ex] |
| [34] | Bigi II. TAU 2012 WS, Nuclear Physics B Proceedings Supplement 2013; 1-4. arXiv:1109.1527 [hep-ex] |