RESEARCH ARTICLE
Performance Evaluation on Several Exchange-correlation Functional Ap-proximations in Calculations of Alkali-metals and IB Group Metals Pair Potentials
Zhou S*, Yang L
Article Information
Identifiers and Pagination:
Year: 2015Volume: 2
First Page: 1
Last Page: 10
Publisher Id: PHY-2-1
DOI: 10.2174/1874843001502010001
Article History:
Received Date: 4/12/2014Revision Received Date: 2/3/2015
Acceptance Date: 24/3/2015
Electronic publication date: 15/5/2015
Collection year: 2015
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
Abstract
In the present paper, inter-atomic pair potentials in alkali-metals and IB group metals, in crystal state and diatomic system, respectively, are systematically calculated by means of electronic density functional theory with several exchange-correlation (EC) functional approximations. In the absence of experimental potential function information, experimentally available bonding length and binding energy of crystal lattice structure, and equilibrium separation and potential minimum of diatomic systems, are used for the first time in the context of potential energy as a function of atom separation, to evaluate the performance of the EC approximations considered in calculating the main properties of neutral atom potential energy curve. Comparison between the experiment measures and first-principle calculations indicates that (i) all EC functional approximations show great changes in their performances for different systems, and the performances of a given EC functional approximation are variable even for the same element but different structures. (ii) The EC functional approximations considered show relatively stronger adaptability in calculations for the crystal lattice structures of both alkali-metals and IB metals, but the performances for the IB metals Cu, Ag, Au diatomic systems degrade somewhat; more than that, the alkali-metal Li, Na, K, Rb, and Cs diatomic systems are inexorably the most difficult to be dealt with by all EC approximations considered. (iii) Although the calculated inter-atomic pair potentials in the diatomic system comprised of the IB metals and alkali-metals, respectively, display unmistakable deviations from the experimental measures, they still constitute specific empirical materials on which effective inter-atomic pair potentials are constructed to take into account the three-body interactions in the statistical mechanics theory considering only two-body interactions.
1. INTRODUCTION
Inter-particle interaction potential function is the most basic input information of any statistical mechanics theories [1], and computer simulation like Monte-Carlo simulation and molecular dynamic simulation [2]. The main differentiation between the computer simulations and statistical mechanics theories lies in “exactness” of the computer simulations results and approximation of the statistical mechanics theories predictions for any given model potentials used as input. It is well-known that validity of the model potential function determines the applicability of computer simulation results to properties of materials whose inter-particle interactions the potential functions used are originally devised to model; on the other hand, reliability of the model potential functions is really critical for the statistical mechanics theories to predict well for real materials given that the theories are essentially approximate.
There are two ways used to obtain the inter-particle potential function information. One way is a theoretical route which constructs the pair potential by a detailed quantum-mechanical calculation, and usually a density functional theory (DFT) is employed to simplify the calculations; however, approximations are thus introduced into the calculation results as the cost of reduced computational capacity. Another way is an experimental one by which pair interaction at all separations can be extracted from a study of any process that involves collisions between molecules. One commonly used procedure is to assume a specified form for the pair potential and determine the relevant parameters by measured values of virial coefficients in the gas phase or transport properties. In this way, an energy parameter ε and a size parameter σ in the Lennard-Jones pair potential have been determined for a large number of light gases, noble gases, simple polyatomic gases, inorganic and organic vapors, and hydrocarbons, and besides, relevant potential parameters in the square-well potential, Buckingham-Corner potential, modified Buckingham (6-exp) potential, Stockmayer potential, etc. have also been established for molecules of some substances [3]. It should be noted that besides the virial coefficients and transport properties experimentally measured values of other thermophysical properties such as elastic constants in crystalline phase, pair correlation function and structure factor, vapor-liquid coexistence line, saturation pressure and critical point parameters, isobar at liquid phase, equilibrium compressibility as well as thermal expansion as a function of temperature, etc. are also proper to be adapted for specification of the potential parameters [4].
In this work we will calculate the pair interaction potentials in alkali-metals and IB group metals by applying an electronic density functional theory (DFT) under several different density functional approximations (DFAs) for an exchange-correlation (EC) energy functional; by comparing the calculated bond length, bond energy, equilibrium separation, and potential minimum with corresponding experimental measurements available in literatures, effectiveness of the DFAs used in calculating the main features of atomic pair potentials in crystal state or diatomic system will be determined and the role of electronic DFT in constructing the full atomic pair potentials will be explored. In the assessment of DFAs, great weight is usually given to the accuracy of molecular atomization energies or the enthalpies of formation constructed from calculated atomization energies; the physical quantities serving as benchmark tools for evaluation of the DFAs also include ionization energies of atoms, correlation energies of atoms and molecules, chemisorption energies, electronegativities for the neutral atoms, surface energies, bulk properties of solids like lattice constant, bulk moduli, phonon frequencies, magnetism, and ferroelectricity, and so on. In the present work, by concentrating on the inter-atomic potential energy curve calculations by eight kinds of the most common DFAs, specific empirical materials for performance evaluation of the DFAs for the EC energy functional will be obtained, and may be considered as selection criteria of the EC energy functional approximations in relevant fields.
The rest of this paper is organized as follows: In section II, a brief review of several favorite EC functional approximations is presented and applied to calculate inter-atomic pair potentials of alkali-metal Li, Na, K, Rb, Cs and IB metal Cu,Ag,Au, in crystal lattice structure and diatomic systems, respectively. In section III, the calculated full pair potentials are presented, and their main features as of the potential minimum and corresponding inter-atomic separation are compared with experimental measurements to evaluate the ability of particular EC functional approximations to adapt to calculation of inter-atomic pair potential characteristics. Finally, we analyze, in section IV, the role of DFT-based calculations in constructing full atom pair potential suitable for modeling thermophysical properties of particular materials.
2. REVIEW OF EXCHANGE-CORRELATION FUNCTIONAL APPROXIMATIONS
Kohn-Sham density functional theory (DFT) [5] is widely used for self-consistent electronic structure calculations of the ground-state properties of atoms, molecules, and solids. In this theory, only the EC energy EXC as a functional of the electron density must be known; due to the nonlinearity and complexity of many-body problems, exact form of is never known, and various approximations are thus introduced to make tractable. The most popular functional approximations include local density approximation (LDA) appropriate for slowly varying density [5], and a generalized gradient approximation (GGA) [6, 8] typically favoring density inhomogeneity more than LDA does. It has long been realized that the molecular bond energies and the cohesive energies of the solids are overestimated when the electronic exchange and correlation effects are described in the LDA [5]. However, the development of nonlocal GGA has demonstrated that the bond energies of molecules, the cohesive energies of solids, and the energy barriers for molecular reactions can be greatly improved within the DFT framework [7, 8]. Different versions of the GGA are available currently, and they include PW91 [8], PBE [9], RPBE [10], HCTH [11], BLYP [12], PBEsol [13], WC [14], and some others. Each approximation for has its own specific fields of use, and it is noted that (i) although the PW91 improves the calculation of atomic energies over the LDA results, it does not give a consistent improvement over LDA results when applied to bulk properties of solids; moreover, the PW91 has its own internal defects as discussed in literature [15]. (ii) The PBE is the most commonly used in solid state calculations, but its deficiency is very clear: while LDA often slightly underestimates equilibrium lattice constants by about 1%, PBE usually overestimates them by about the same amount. Other equilibrium properties, such as bulk moduli, phonon frequencies, magnetism, and ferroelectricity, are sensitive to the lattice constant, and so are also overcorrected by the PBE [16]; particularly, surface energies are too low in LDA, but are made lower still by the PBE [17]. (iii) The RPBE functional only differs from the PBE functional in the choice of the mathematical form for the exchange energy enhancement factor, and therefore they contain the same physics and fulfill the same physical criteria. The RPBE functional improves chemisorption energies of atoms and molecules on late transition-metal surfaces, which are overestimated by the LDA, PW91 and PBE functionals. (iv) The WC gives significant improvements for lattice constants, crystal structures, and metal surface energies over the most popular PBE, and there are no adjustable parameters; however, it is less accurate for atoms than the PBE and RPBE. (v) The HCTH functional is a semi-empirical one, and the parameters involved in the functional are determined by a least-squares optimization procedure using a limited training set of molecular data, and are in principle for all molecules as one is able to obtain accurate descriptions of comparable systems that are absent from the training set, and the accuracy is comparable to other DFT calculations. The HCTH functional has been shown to perform well to several chemical problems compared to other functional approximations, with an accuracy only surpassed by very few hybrid functional approximations which include exact exchange. (vi) Both the PBE and PBEsol are first-principles GGAs, the main difference between them is that they are based upon different selections of exact constraints to satisfy. At the GGA level, but not at the higher meta-GGA level, one can at most satisfy two out of the following three constraints exactly: (I) second-order gradient expansion for exchange, (II) second-order gradient expansion for correlation, (III) LSD-like linear density response of a uniform electron gas. The PBE satifies (II) and (III) but not (I), whereas the PBEsol satisfies (I) and compromises between (II) and (III). From the performance perspective, the PBEsol describes more correctly the stereoelectronic (SE) effects in many hydrocarbons than many other DFT functional approximations, applies to densely packed solids, and is also useful for large organic molecules (in the absence of free atoms) [18]. On the other hand, although no GGA without a dispersion correction can account for long-range correlation, the PBEsol (after the error cancelation between exchange and correlation) can apparently account for medium-range interaction better than the PBE [19]. (vii) The BLYP functional achieves an average error on the G2 and G3 sets of small molecule experimental atomization energies of 6.17 and 7.60 kcal/mol, respectively [20], and this is a very respectable performance, particularly as compared with the LDA; however, it is important to note that the larger errors in the G3 set typically occur for bigger molecules, where errors in individual bond energies can accumulate. Due to the computational expense of the exact exchange, calculations using hybrid functionals can be very expensive compared to the pure GGA functionals; solid-state calculations are also quite inefficient with hybrid functional approximations. On the other hand, the LDA is the simplest approximation, constructed from uniform electron gas. Although valid in principle only for slowly varying densities, the LDA has met with impressive practical success for solids, where the valence electron densities vary relatively more slowly than in molecules and atoms. However, the LDA, as is well known, is not suitable for the binding energy of molecule, and it also underestimates the equilibrium lattice constant a0 by 1%-3%. As some properties such as ferroelectricity are extremely sensitive to volume, when calculated at the LDA volume, the ferroelectric instability is severely underestimated.
In the final analysis, one can arrive at the conclusion that each of the current EC functional approximations has its own validity application range, none could be applied with great accuracy to calculations of all properties. In fact, due to a degree of experiences in the constructions of the EC approximations, it does not seem to be such a very easy matter to predict the performance of any particular EC approximation on given property; consequently, simple and effective method is testing each EC approximation based on a series of comparisons with experimental measures.
3. RESULTS AND DISCUSSION
The molecular simulation package used in our study is Materials Studio, which is developed by Accelrys, Inc. In computation, we use the plane wave expansion to describe wave function of the electron. To reduce number of the plane waves used, we employ pseudo potential to reset the real atomic potential energy. In calculating the interatomic potential in metal diatomic systems, we employ the Dmol3 module, wherein the selected basis set is double numerical plus d functions, the self-consistent field (SCF) tolerance is set to 10-5ev/atom, and a DIIS algorism (direct inversion in an iterative subspace) is employed to quicken and stabilize the convergence process. In Dmol3, core treatment employs an effective core potential and all electron basis set of relativity. In calculating the inter-atomic potential in crystal lattice structure, Castep module is used, which employs plane wave basis set with an energy cutoff of plane wave calculation in reciprocal space being set to 330ev, the SCF tolerance is set to 10-6ev/atom, k-point in the Brillouin zone is set to 12×12×12, and ultrasoft pseudo potential is employed.
3.1. Inter-atomic Potential Function in Crystal Lattice Structure
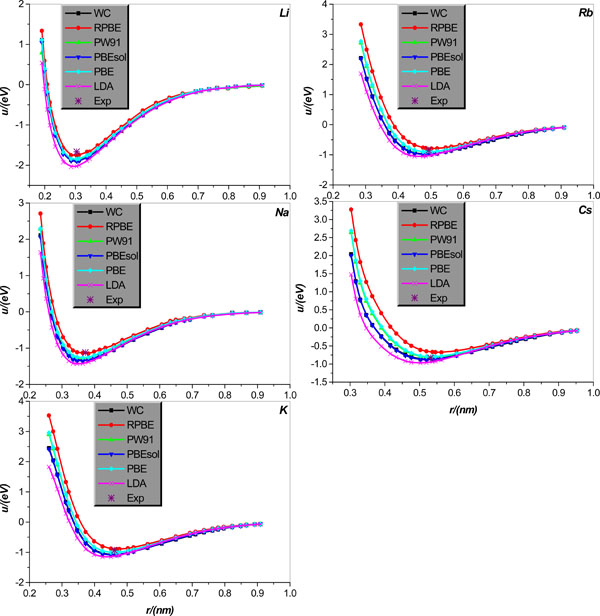
Inter-atomic potential function u(r) in crystal lattice structure will first be studied. Specifically, we will calculate u(r) for body centered cubic alkali-metal Li, Na, K, Rb, Cs and IB face-centered cubic metal Cu, Ag, Au. The relevant results calculated theoretically, collected in literature [21], are graphically displayed in Figs. (1 and 2), together with the corresponding experimental values of bonding length and binding energy, collected in Tables 1 and 2.
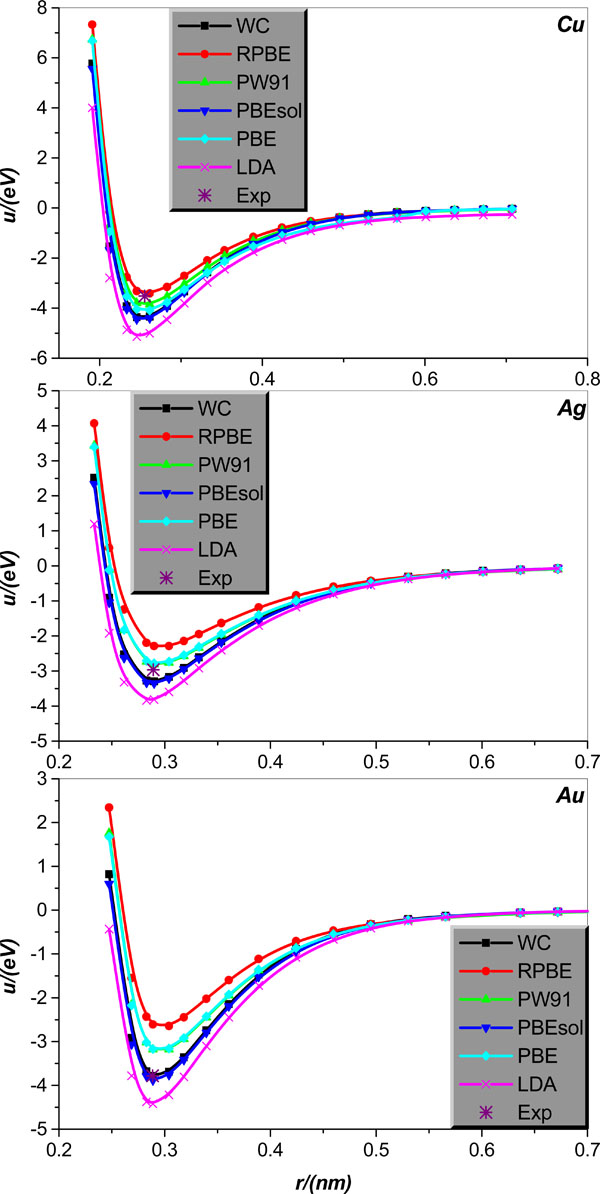 |
Fig. (2). Same as in Fig. 1 but for the IB face-centered cubic metal Cu, Ag, and Au crystal lattice structures. |
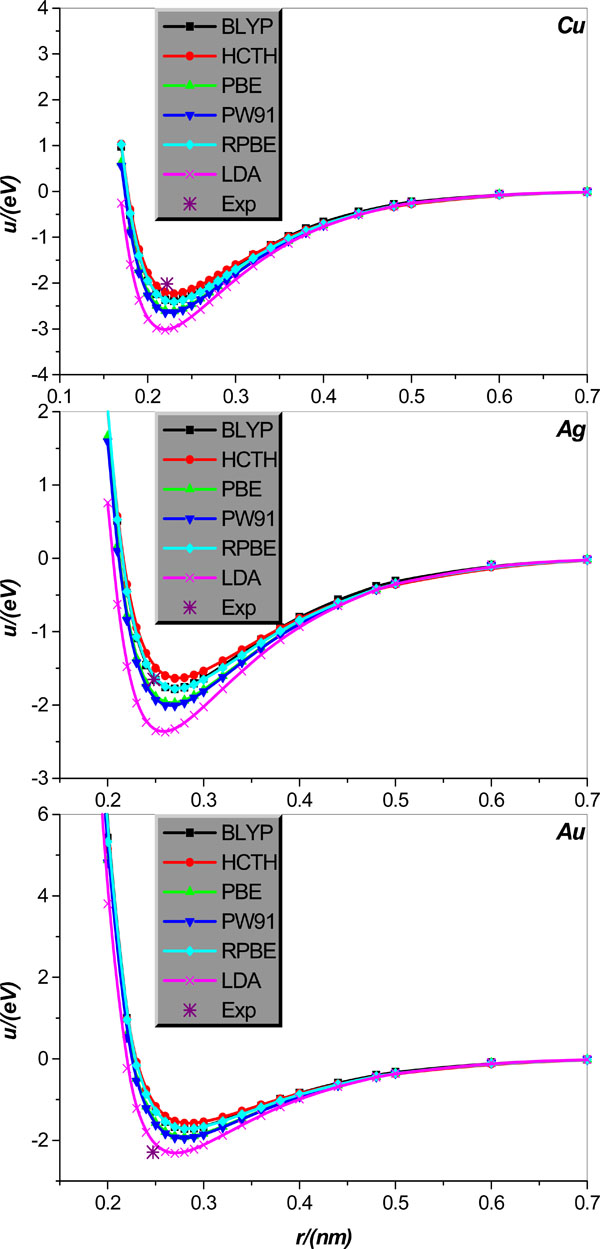 |
Fig. (4). Same as in Fig. (3) but for the alkali-metal Cu, Ag, and Au diatomic systems. |
Body centered cubic alkali-metal Li, Na, K, Rb, and Cs bonding length and binding energy experimental values [23].
| Li | Na | K | Rb | Cs | |
|---|---|---|---|---|---|
| Bonding length /(nm) | 0.304 | 0.3074 | 0.4544 | 0.495 | 0.5308 |
| Binding energy /(eV) | 1.615 | -1.092 | -0.895 | 0.820 | -0.770 |
IB face-centered cubic metal Cu, Ag, and Au crystal lattice structure bonding length and binding energy experimental values [23].
| Cu | Ag | Au | |
|---|---|---|---|
| Bonding length /(nm) | 0.2556 | 0.2888 | 0.2884 |
| Binding energy /(eV) | 3.399 | 2.859 | 3.679 |
Equilibrium distance and potential minimum experimental values of Alkali-metal Li, Na, K, Rb, and Cs diatomic systems.
| Li | Na | K | Rb | Cs | |
|---|---|---|---|---|---|
| Equilibrium distance /(nm) | 0.26729 [24] | 0.30788 [24] | 0.39051 [24] | 0.4082 [25, 26] | 0.4470 [24] |
| Potential minimum /(eV) | 1.07 [26] | 0.774 [26] | 0.575 [26] | 0.458 [26] | 0.420 [26] |
Equilibrium distance and potential minimum experimental values of IB metal Cu, Ag, and Au diatomic systems.
| Cu [27] | Ag [27] | Au [27] | |
|---|---|---|---|
| Equilibrium distance /(nm) | 0.22197 | 0.2480 | 0.24719 |
| Potential minimum /(eV) | 2.020 | 1.65 | 2.29 |
It should be pointed out that there is not experimental potential function information over an entire separation range, we only can evaluate the two main properties of the calculated potential energy curve, i.e. minimum and relevant distance of the potential energy curve, by using experimentally available bonding length and binding energy of crystal lattice structure, and equilibrium separation and potential minimum of diatomic systems.
It is shown that (i) the LDA obviously underestimates the bonding length and overestimates the binding energy of all body centered cubic alkali-metal Li, Na, K, Rb, Cs. (ii) All GGA type EC functional approximations considered give relatively reliable estimation of all body centered cubic alkali-metal bonding lengths, but their performance in calculating these alkali-metals binding energy presents evident disparity. To be specific, for Li, Na, only the RPBE is accurate for the calculation of binding energy, and other EC approximations overestimate the binding energies of these two metals. For alkali-metal K, both WC and PBESOL evidently overestimate the binding energy of K. Encouragingly, RPBE, PW91, and PBE can give K binding energy in good agreement with corresponding experimental value; among the three approximations, RPBE underestimates the binding energy, while both PW91 and PBE slightly overestimate it. For alkali-metal Rb, both PBE and PW91 can accurately calculate the Rb binding energy; however, RPBE underestimates it and both WC and PBESOL overestimate the Rb binding energy. For alkali-metal Cs, both WC and PW91 predict the Cs binding energy in very good agreement with the corresponding experimental value; however, both RPBE and PBE underestimate the Cs bonding energy, and PBESOL overestimates it slightly.
Now we turn the discussion to the IB metal Cu, Ag, Au. Fig. (2) clearly illustrates that the LDA pretty seriously overestimates the binding energies of three IB metal Cu, Ag, Au, and slightly, but still observably underestimates their bonding lengths. As for the GGA, all considered EC functional approximations under the name of GGA give rather reliable estimations of the IB metal Cu, Ag, Au bonding lengths; however, their performances in calculating the binding energy of the IB metals differ greatly. More specifically, for metal Cu, only RPBE can give more accurate estimation of the binding energy, and all other EC approximations are considered to overestimate it. For metal Ag, both PW91 and PBE perform well for the calculation of Ag binding energy, but the RPBE obviously underestimates and both the PBESOL and WC clearly overestimate it, respectively. Finally, for metal Au, both the WC and PBESOL are surprisingly successful in calculating the Au binding energy, but the PBE, RPBE, and PW91 unfortunately underestimate dramatically this quantity.
3.2. Interatomic Potential in Metal Diatomic Systems
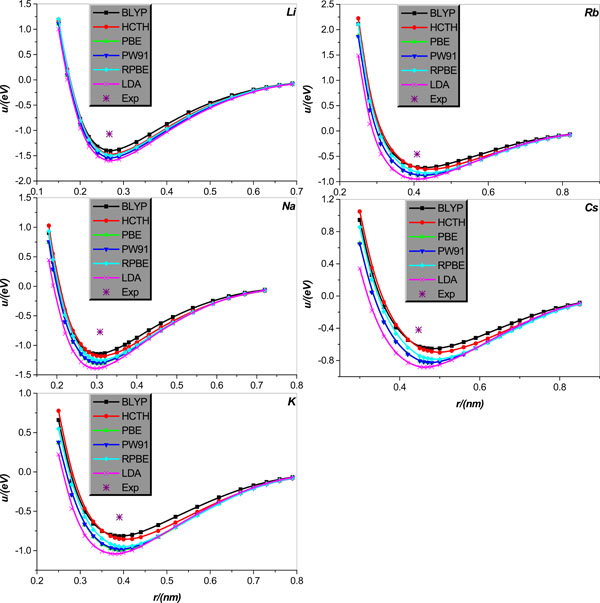
We calculate the inter-atomic potentials in alkali-metal atoms Li, Na, K, Rb, and Cs, and IB metal atoms Cu, Ag, and Au in diatomic systems, respectively, and display the results, collected in literature [21], in Figs. (3 and 4); for comparison, the corresponding experimental values of the equilibrium distance and potential minimum, collected in Tables 3 and 4, are also shown.
We first analyze the situations of alkali-metal Li, Na, K, Rb, and Cs diatomic system. Fig. (3) clearly shows that all EC functional approximations considered the potential minimum of all alkali-metal diatomic systems, but by comparison, BLYP is relatively more accurate. As regards the calculation of the equilibrium distance, it is shown that the equilibrium distances of Li, Na, and K can be calculated accurately by all EC functional approximations considered except that the LDA slightly underestimates the Na and K equilibrium distances. For the Rb and Cs situations, all EC approximations overestimate the equilibrium distances except that the LDA very accurately predicts the Rb equilibrium distance; in particular, the relative accuracy of the EC approximations considered increases in order of the HCTH, RPBE, PW91, BLYP and LDA.
Now we turn the attention to diatomic systems comprised of IB metal Cu, Ag, and Au, respectively. Fig. (4) clearly shows that for Cu diatomic system, the HCTH is relatively the most accurate for the potential minimum estimation, but it slightly overestimates the equilibrium distance of Cu. On the other hand, PW91 and LDA are proper for calculation of the equilibrium distance, but both overestimate rather seriously the potential minimum. Finally, the BLYP, PBE, and RPBE are relatively satisfactory for the calculations of both equilibrium distance and potential minimum of the Cu diatomic system. For diatomic system Ag, the RPBE and BLYP are surprisingly accurate for the potential minimum calculation, at the same time both only slightly overestimates the equilibrium distance. Remarkably, performance of the LDA shows some discrepancy between the equilibrium distance and potential minimum descriptions; on the one hand LDA is relatively the most precise for the equilibrium distance calculation, but on the other hand it overrates the potential minimum very seriously. Finally, other EC functional approximations considered such as the HCTH, PBE and PW91, all overestimate the potential minimum of metal Ag to varying degrees, and almost the same degree overestimate the equilibrium distance. For diatomic system Au, all EC functional approximations considered overrate the equilibrium distance of the Au diatomic system; among the six approximations used, the BLYP, HCTH, PBE, RPBE, and PW91 are the least reliable, whereas the LDA calculation gives some improvement on the former five approximations. By comparison, the LDA is the most accurate one in calculating the diatomic Au potential minimum, and other EC functional approximations considered all underestimate it pretty obviously and to varying degrees as graphically shown in Fig. (4).
It should be pointed out that what is computed in the crystal case is an effective pair potential, which embodies the roles played by many body interactions (three, four,… -body). This is clear from a comparison between Figs. (1, 3) and Figs. (2, 4), which shows that the potential curves calculated by the same EC approximation and for the same element but different structures (crystal and dimmer, respectively) differ from each other, and the difference is particularly clear for smaller atom separations and seems more and more unobservable for larger atom separation. It is also noted that minimum and relevant distance of the pair potential for the crystal structures are not compatible with the experimental cohesive energies and the nearest neighbor (NN) distance, as the cohesive energies include the zero point vibrational energy as well as the inter-atom interaction energies at equilibrium positions, and the NN distance is actually an average inter-particle separation.
CONCLUSION
Regarding first-principle calculations of the interatomic potentials of alkali-metal Li,Na,K,Rb,and Cs, and IB metal Cu,Ag,and Au, in crystal lattice structure and diatomic systems, respectively, systematic studies have been conducted in the present paper by employing a range of existing EC functional approximations in the electronic DFT framework, and related conclusions are drawn as follows.
1 All EC functional approximations show great changes in their performances for different systems, and the performances of a given EC functional approximation are variable even for the same element but different structures. In particular, the EC functional approximations show relatively stronger adaptability in calculations for the crystal lattice structures of both alkali-metals and IB metals, but the performances for the IB metals Cu, Ag, Au diatomic systems degrade somewhat. Unfortunately, the alkali-metal Li, Na, K, Rb, and Cs diatomic systems are inexorably the most difficult to be dealt with by all EC approximations considered, and for these objects locations of the experimental data point and the extreme point of the relevant potential energy curve are visually apart to varying degrees, as graphically shown in Fig. (3). From the Fig. (3) one learns that these difference stem from either only a disagreement between the potential minimum from the two routes or disagreements between both the equilibrium distance and potential minimum from the two routes, respectively.
As regards origin of differences between the performances of various EC approximations and between the calculations and the experimental measurements, especially in the case of diatomic systems, it might be worth a little analysis. Although Hohenberg-Kohn theorem proves existence of the EC functional, its exact expression is never known; as a result, approximate expressions are resorted, and errors are introduced into the final results. Thus, the differences between the calculations and the experimental measurements are explained. As different systems have ever-changing form of the electronic density, a universally valid EC approximation is actually impossible. However, physical meaning of the EC functional is clear, and it is possible to assume an expression with physical basis and involved with several adjustable parameters, which are determined by sum rules and small system data. As a result, there exist many EC approximations with differences in emphasis point of physical picture, sum rules, and built-in experimental data, and consequently, performance differences of these EC approximations in different systems are in reason. It is noted that in the case of diatomic systems, the EC approximations considered generally degrade even quite obviously. Generally speaking, the more gently the electronic density changes spatially, the more easily the EC functional is approximated. For crystal lattice system, periodic arrangement of the atomic cores makes the space distribution of the total potential field changes gently, and the resulting electronic density profile also changes gently. On the contrary, the two-atom system lacks periodic arrangement, the total potential field, and correspondingly, the resulting electronic density is relatively more uneven. As a result, the EC approximations show greater inadaptability in the two-atom system than in the crystal lattice system.
Fortunately, the unsatisfactory performance in the diatomic systems does not constitute a big trouble in predicting thermodynamic properties based on statistical mechanics theory and the pair potential of the diatomic systems as the statistical mechanics calculations, on the other hand, is a very different story, wherein what is used directly as input is not the first-principle calculation pair potential itself, as covered in more detail below.
2 Although the different EC approximations behave very differently in almost all cases when compared to the experimental results, either of them depicts the common characteristics of the van der Waals force between neutral atoms (called dispersion force), i.e. short-range repulsion and long-range attraction. On the other hand, we only consider the pair potential between two atoms in the dimmer case in so far; however, a three-body potential arises because the electron clouds in two atoms near one another readjust in response to a third atom coming into their neighborhood. Although the three-body interactions are much smaller than the two-body contribution, they cannot be neglected for most cases. When the three-body interactions are present, they have to be transformed into a form of pair potential to be superimposed above the pair potential to be tractable within the traditional statistical mechanics theoretical framework. As a result, the pair potential entering the ready-made machinery of statistical mechanics to produce macroscopic thermodynamic properties is not the pair potential based on the first-principle calculations, but the one that is similar to the first-principle pair potential and takes several parameters to adjust for enforcing the agreement between statistical mechanics calculations and experimental measurements of relevant thermodynamic properties such as critical point, vapor-liquid coexistence curve, triple point, and etc. A typical example of the method is demonstrated in a recent publication [22] dealing with iron, copper and sodium. Considering that the first-principle pair potential is subject to be revised and adjusted to take into account the three-body interactions, and consequently, further approximations are introduced, the inaccuracy of first-principle pair potential does not create trouble in predicting macroscopic properties given that all EC approximations considered catch the main characteristics of the pair potentials.
3 By the analysis of above second point, one has reasons to believe that the interatomic potentials in diatomic systems of alkali-metal Li, Na, K, Rb, and Cs, and IB metal Cu, Ag, and Au, respectively, provided by this paper, offers reliable first-principle data to help in raising the quality and reducing the empirical element for the empirical pair potential model constructed to be used in the ready-made machinery of statistical mechanics, and we will report relevant studies in separate papers.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGMENTS
The authors would like to thank the anonymous reviewers for their contributions in helping revise the paper. This project is supported by the National Natural Science Foundation of China (Grants 21173271 and 21373274).
REFERENCES
| [1] | (i) Henderson D. Fundamentals of inhomogeneous fluids New York; Marcel Dekker 1992.; (ii) Martynov GA. Fundamental theory of liquids Method of distribution functions Bristol Adam Hilger 1992.; (iii) Hansen J-P, McDonald IR. Theory of Simple Liquids 3rd ed London Academic Press 2006. |
| [2] | (i) Frenkel D, Smit B. Understanding molecular simulation Boston MA Academic Press 2001.; (ii) Leach AR. Molecular modelling principles and applications North America North American Pearson Education Limited 2001. |
| [3] | Hirschfelder JO, Curtiss CF, Bird RB. Molecular theory of gases and liquids New York Wiley 1954. |
| [4] | (i) Girifalco LA, Weizer VG. Application of the Morse potential function to cubic metals Phys Rev 1959; 114: 687-90.; (ii) Kniaz K, Girifalco LA, Fischer JE. Application of a spherically averaged potential to solid C70 in the disordered phase J Phys Chem 1995; 99: 16804-6.; (iii) Girifalco LA. Extended Mie-Grüneisen theory applied to C60 in the disordered fcc phase Phys Rev B 1995; 52: 9910-16.; (iv) Lundin A, Sundqvist B. Compressibility of C60 in the temperature range 150-335 K up to a pressure of 1 GPa Phys Rev B 1996; 53: 8329-36. |
| [5] | (i) Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects Phys Rev 1965; 140: A1133.; (ii) Jones RO, Gunnarsson O. The density functional formalism, its applications and prospects Rev Mod Phys 1989; 61: 689-746. |
| [6] | (i) Langreth DC, Mehl MJ. Beyond the local-density approximation in calculations of ground-state electronic properties Phys Rev B 1983; 28: 1809-34.; (ii) Becke AD. Density-fnnctional exchange-energy approximation with correct asymptotic behavior Phys Rev A 1988; 38: 3098-100. |
| [7] | (i) Kong XJ, Chan CT, Ho KM, Ye YY. Cohesive properties of crystalline solids by the generalized gradient approximation Phys Rev B 1990; 42: 9357-64.; (ii) Ortiz G. Gradient-corrected pseudopotential calculations in semiconductors Phys Rev B 1992; 45: 11328-31.; (iii) Garcia A, Elsässer C, Zhu J, Louie SG, Cohen ML. Use of gradient-corrected functionals in total-energy calculations for solids Phys Rev B 1992; 46: 9829-32.; (iv) Novikov DL, Freeman AJ, Christensen NE, Svane A, Rodriquez CO. LDA simulations of pressure-induced anomalies in c/a and electric-field gradients for Zn and Cd Phys Rev B 1997; 56: 7206-14.; (v) Philipsen PHT, te Velde G, Baerends EJ. The effect of density-gradient corrections for a molecule-surface potential energy surface Slab calculations on Cu(100)c(2x2)-co Chem Phys Lett 1994; 226: 583-8.; (vi) Hu P, King DA, Crampin S, Lee MH, Payne MC. Gradient corrections in density functional theory calculations for surfaces Co on Pd(110) Chem Phys Lett 1994; 230: 501-6.; (vii) White JA, Bird DM, Payne MC, Stich I. Surface Corrugation in the Dissociative Adsorption of H2 on Cu(100) Phys RevLett 1994; 73: 1404-7. |
| [8] | Perdew JP, Chevary JA, Vosko SH , et al. Atoms, molecules, solids, and surfaces Applications of the generalized gradient approximation for exchange and correlation Phys Rev B 1992; 46: 6671-87. |
| [9] | Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple Phys Rev Lett 1996; 77: 3865-8. |
| [10] | Hammer B, Hansen LB, Nørskov JK. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals Phys Rev B 1999; 59: 7413-21. |
| [11] | (i) Hamprecht FA, Cohen AJ, Tozer DJ, Handy NC. Development and assessment of new exchange-correlation functionals J Chem Phys 1998; 109: 6264-71.; (ii) Boese AD, Doltsinis NL, Handy NC, Sprik M. New generalized gradient approximation functionals J Chem Phys 2000; 112: 1670-8.; (iii) Boese AD, Handy NC. A new parametrization of exchange-correlation generalized gradient approximation functionals J Chem Phys 2001; 114: 5497-03. |
| [12] | (i) Becke AD. Density-fnnctional exchange-energy approximation with correct asymptotic behavior Phys Rev A 1988; 38: 3098-100.; (ii) Lee C, Yang W, Parr RG. Development of the Colic-Salvetti correlation-energy formula into a functional of the electron density. Phys Rev B 1988; 37: 785-9. |
| [13] | (i) Perdew JP, Ruzsinszky A, Csonka GI , et al. Restoring the density-gradient expansion for exchange in solids and surface Phys Rev Lett 2008; 100: 136406--4.; Erratum Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces [Phys Rev Lett 100 136406 (2008)] 2009; 102: 039902(E). |
| [14] | Wu Z, Cohen RE. More accurate generalized gradient approximation for solids Phys Rev B 2006; 73: 235116-1-6. |
| [15] | Juan YM, Kaxiras E. Application of gradient corrections to density-functional theory for atoms and solids Phys Rev B 1993; 48: 14944-52. |
| [16] | Wu Z, Cohen RE. More accurate generalized gradient approximation for solids Phys Rev B 2006; 73: 235116-1-6. |
| [17] | Constantin LA, Perdew JP, Tao J. Meta-generalized gradient approximation for the exchange-correlation hole with an application to the jellium surface energy Phys RevB 2006; 73: 205104-1-11. |
| [18] | Csonka GI, Ruzsinszky A, Perdew JP, Grimme S. Improved description of stereoelectronic effects in hydrocarbons using semilocal density functional theory J Chem Theory Comput 2008; 4: 888-91. |
| [19] | Csonka GI, Perdew JP, Ruzsinszky A , et al. Assessing the performance of recent density functionals for bulk solids Phys Rev B 2009; 79: 155107--14. |
| [20] | Curtiss LA, Raghavachari K, Redfern PC, Pople JA. Assessment of Gaussian-3 and density functional theories for a larger experimental test set J Chem Phys 2000; 112: 7374-83. |
| [21] | See supplementary material at http://benthamopen.com/contents/supplementary-material/PHY-2- 1_SD1.pdf for the potential functions calculated theoretically for alkali-metal Li Na K Rb Cs and IB metal Cu Ag Au in crystal lattice structure and diatomic system |
| [22] | Apfelbaum EM. The calculation of vapor-liquid coexistence curve of Morse κuid application to iron J Chem Phys 2011; 134: 194506--7. |
| [23] | Li Z-H, Ed. Data book of the element Properties Hebei People's Republishing House Press. 1985. |
| [24] | Huber KP, Herzberg G, Eds. Constants of diatomic molecules New York Van Nostrand Reinhold. 1979. |
| [25] | Zhang MB, Zhao DX, Yang ZZ. The characteristic boundary radii of atoms J Theor Comput Chem 2005; 4: 281-88. |
| [26] | Dean JA, Ed. Lange’s Handbook of Chemistry 15th ed New York McGraw Hill Inc. 1999. |
| [27] | Ho J, Ervin KM, Lineberger WC. Photoelectron spectroscopy of metal cluster anions Cu-n, Ag-n, and Au-n J Chem Phys 1990; 93: 6987-7002. |