RESEARCH ARTICLE
Diffractive Cross Sections Implemented in PYTHIA8-MBR vs LHC Results§
Konstantin Goulianos*
Article Information
Identifiers and Pagination:
Year: 2014Volume: 1
Issue: Suppl 1: M11
First Page: 72
Last Page: 74
Publisher Id: PHY-1-72
DOI: 10.2174/1874843001401010072
Article History:
Received Date: 25/11/2013Revision Received Date: 24/01/2014
Acceptance Date: 25/1/2014
Electronic publication date: 31/12/2014
Collection year: 2014
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
Abstract
We review the predictions of diffractive cross sections implemented in the PYTHIA8-MBR Monte Carlo simulation and compare them to recent LHC results.
PACS Number(s): 12.40.Nn, 12.39.St, 13.85.Lg, 13.85.Fb.
1. INTRODUCTION
Measurements at the LHC
have shown that there are sizable disagreements among Monte Carlo (MC)
implementations of “soft” processes based on cross sections proposed by various
physics models, and that it is not possible to reliably predict all such
processes, or even all aspects of a given process, using a single model [1-3].
In the CDF studies of diffraction at the Tevatron, all processes are well
modeled by the MBR (Minimum Bias Rockefeller) MC simulation, which is a
stand-alone simulation based on a unitarized Regge-theory model, RENORM [4],
employing inclusive nucleon parton distribution functions (PDF’s) and QCD color
factors. The RENORM model was updated in a presentation at EDS-2009 [5] to
include a unique unitarization prescription for predicting the total
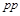 cross section at high energies, and
that update has been included as an MBR option for simulating diffractive
processes in PYTHIA8 since version PYTHIA8.165 [6], to be referred here-forth
as PYTHIA8-MBR. In this paper, we briefly review the cross sections [7]
implemented in this option of PYTHIA8 and compare them with LHC measurements.
cross section at high energies, and
that update has been included as an MBR option for simulating diffractive
processes in PYTHIA8 since version PYTHIA8.165 [6], to be referred here-forth
as PYTHIA8-MBR. In this paper, we briefly review the cross sections [7]
implemented in this option of PYTHIA8 and compare them with LHC measurements.
The PYTHIA8-MBR option
includes a full simulation of the hadronization of the implemented diffraction
dissociation processes: single, double, and central diffraction. In the MBR simulation
used at CDF, the hadronization of the final state(s) was based on a data-driven
phenomenological model of multiplicities and
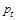 (transverse
momentum) distributions calibrated using S
(transverse
momentum) distributions calibrated using S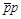 S
and Fermilab fixed-target results. Later, the model was successfully tested
against Tevatron minimum bias (MB) and diffraction data. However, only
S
and Fermilab fixed-target results. Later, the model was successfully tested
against Tevatron minimum bias (MB) and diffraction data. However, only
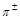 and
and 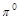 particles
were produced in the final state, with multiplicities obeying a statistical
model of a modified Gamma distribution function that provided good fits to
experimental data [8]. This model could not be used to predict
specific-particle final states. In the PYTHIA8-MBR implementation,
hadronization is perfor-med by PYTHIA8 tuned to reproduce final-state distribut-ions
in agreement with MBR's, with hadronization done in the PYTHIA8 framework.
Thus, all final-state particles are now automatically produced, greatly
enhancing the horizon of applicability of PYTHIA8-MBR.
particles
were produced in the final state, with multiplicities obeying a statistical
model of a modified Gamma distribution function that provided good fits to
experimental data [8]. This model could not be used to predict
specific-particle final states. In the PYTHIA8-MBR implementation,
hadronization is perfor-med by PYTHIA8 tuned to reproduce final-state distribut-ions
in agreement with MBR's, with hadronization done in the PYTHIA8 framework.
Thus, all final-state particles are now automatically produced, greatly
enhancing the horizon of applicability of PYTHIA8-MBR.
2. CROSS SECTIONS
The following diffraction dissociation processes are considered in PYTHIA8-MBR:
SD 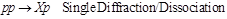 (1)
(1)
or 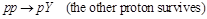
DD 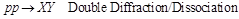 (2)
(2)
CD/DPE 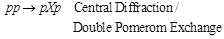 (3)
(3)
The RENORM predictions
are expressed as unitarized Regge-theory formulas, in which the unitarization
is achi-eved by a renormalization scheme where the Pomeron (IP)
flux is interpreted as the probability for forming a diffractive (non-exponentially
suppressed) rapidity gap and thereby its integral over all phase space
saturates at the energy where it reaches unity. Differential cross sections are
expressed in terms of the IP-trajectory,
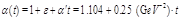 , the IP-p coupling,
, the IP-p coupling,
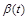 ,
and the ratio of the triple-IP to the IP-
,
and the ratio of the triple-IP to the IP-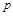 couplings,
couplings,
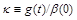 . For large rapidity gaps,
. For large rapidity gaps,
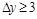 , for which IP -exchange dominates, the cross
sections may be written as,
, for which IP -exchange dominates, the cross
sections may be written as,
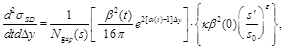 (4)
(4)
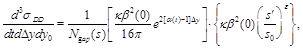 (5)
(5)
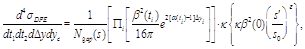 (6)
(6)
where 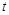 is the 4-momentum-transfer squared at
the proton vertex,
is the 4-momentum-transfer squared at
the proton vertex, 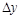 the rapidity-gap width, and
the rapidity-gap width, and
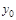 the center of the rapidity gap. In
Eq. (6), the subscript
the center of the rapidity gap. In
Eq. (6), the subscript 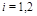 enumerates Pomerons in a DPE
event,
enumerates Pomerons in a DPE
event, 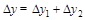 is the total rapidity gap (sum of two
gaps) in the event, and
is the total rapidity gap (sum of two
gaps) in the event, and 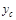 is the center in
is the center in
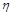 of the centrally-produced hadronic
system.
of the centrally-produced hadronic
system.
The total cross
section (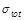 ) is expressed as:
) is expressed as:
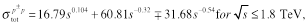 (7)
(7)
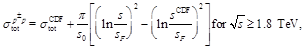 (8)
(8)
where 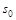 and
and 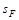 are
energy and the Pomeron flux saturation scales, respectively [7]. For
are
energy and the Pomeron flux saturation scales, respectively [7]. For
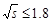 TeV, where there are Reggeon contributions,
we use the global fit expression [9], while for
TeV, where there are Reggeon contributions,
we use the global fit expression [9], while for
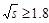 TeV,
where Reggeon contributions are negligible, we employ the Froissart-Martin
formula [10-12]. The two expressions are smoothly matched at
TeV,
where Reggeon contributions are negligible, we employ the Froissart-Martin
formula [10-12]. The two expressions are smoothly matched at
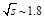 TeV.
TeV.
The elastic cross
section is obtained from the global fit [9] for
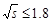 TeV,
while for
TeV,
while for 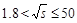 TeV we use an extrapolation of the
global-fit ratio of
TeV we use an extrapolation of the
global-fit ratio of 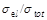 , which is slowly varying
with
, which is slowly varying
with 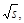 multiplied by
multiplied by
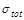 .
The total non-diffractive cross section is then calculated as
.
The total non-diffractive cross section is then calculated as
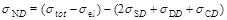 .
.
3. RESULTS
In this section, we present as examples of the predictive power of
the RENORM model some results reported by the TOTEM, CMS, and ALICE collaborations
for pp collisions at 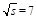 TeV, which can be
directly compared with RENORM formulas without using the PYTHIA8-MBR
simulation.
TeV, which can be
directly compared with RENORM formulas without using the PYTHIA8-MBR
simulation.
Fig. (1, left) shows a comparison of the TOTEM total, elastic, and total-inelastic cross sections, along with results from other experiments fitted by the COMPETE Collaboration [13]; the RENORM predictions, displayed as filled (green) squares, are in excellent agreement with the TOTEM results. Similarly, in Fig. (1, right), good agreement is observed between the ALICE [14] and CMS [15] total-inelastic cross sections and the RENORM prediction.
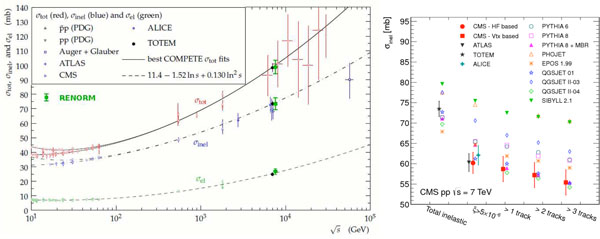 |
Fig. (1). (left) TOTEM measurements of the total, total-inelastic, and elastic pp cross sections at s = 7 TeV shown along with best COMPETE fits [13], with RENORM predictions added as filled squares; (right) ALICE [14] and CMS [15] measurements of the total inelastic cross section at s = 7 TeV show good agreement with the RENORM prediction (PYTHIA8-MBR). |
 |
Fig. (2). Measured SD (left) and DD (right) cross sections for ξ < 0.05 compared with theoretical predictions; the model embedded in PYTHIA8-MBR provides a good description of all data. |
The uncertainty shown in the RENORM prediction of
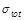 in Fig. (1, left) is
dominated by that in the scale parameter
in Fig. (1, left) is
dominated by that in the scale parameter 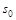 .
The latter can be reduced by a factor of ~4 if
.
The latter can be reduced by a factor of ~4 if
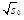 is
interpreted as the mean value of the glue-ball-like object discussed in [16]
and the data shown in figure 8 of [16] are used to determine its value. Work is
in progress to finalize the details of this interpretation.
is
interpreted as the mean value of the glue-ball-like object discussed in [16]
and the data shown in figure 8 of [16] are used to determine its value. Work is
in progress to finalize the details of this interpretation.
Another example of the predictive power of RENORM is shown in Fig.
(2), which displays the total SD (left) and total DD (right)
cross sections for 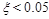 , after extrapolation into
the low mass region from the measured CMS cross sections at higher mass
regions, presented in [17], using RENORM.
, after extrapolation into
the low mass region from the measured CMS cross sections at higher mass
regions, presented in [17], using RENORM.
4. SUMMARY
We reviewed our pre- LHC predictions for the total, elastic, total-inelastic, and diffractive components of the proton-proton cross section at high energies, which are based on a special parton-model approach to diffraction employing inclusive proton parton distribution functions and QCD color factors. We discuss single diffraction/dissociation, double diffraction/dissociation, and central diffraction or double-Pomeron exchange, comparing predictions with LHC measurements. Agreement between data and PYTHIA8-MBR predictions is found in all cases.
CONFLICT OF INTEREST
The author confirms that this article content has no conflicts of interest.
ACKNOWLEDGEMENTS
I would like to thank Robert Ciesielski, my colleague at Rockefeller and collaborator in the implementation of the MBR simulation into PYTHIA8, and the Office of Science of the Department of Energy for supporting the Rockefeller experimental diffraction physics programs at Fermilab and LHC on which this research is anchored.