RESEARCH ARTICLE
Matching the Discrete BFKL Pomeron to DGLAP§
H. Kowalski*, L.N. Lipatov, D.A. Ross
Article Information
Identifiers and Pagination:
Year: 2014Volume: 1
Issue: Suppl 1: M9
First Page: 62
Last Page: 65
Publisher Id: PHY-1-62
DOI: 10.2174/1874843001401010062
Article History:
Received Date: 25/11/2013Revision Received Date: 24/01/2014
Acceptance Date: 25/01/2014
Electronic publication date: 31/12/2014
Collection year: 2014
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
Abstract
The discrete BFKL formalism which accounts for the running of the coupling and incorporates information about the phase of the oscillations at small transverse momentum, arising from the infrared properties of QCD, leads to a QCD pomeron consisting of a set of discrete Regge poles. Here we discuss under what circumstances this discrete pomeron leads to an amplitude which matched the prediction of a DGLAP analysis in the double leading logarithm limit.
1. INTRODUCTION
The BFKL formalism [1] (in the case of zero momentum transfer) considers an amplitude, A(y,t) , for the forward scattering of a gluon with transverse momentum, , with rapidity gap y, which can be treated in terms of its Mellin transform
where C represents a contour taken to the right of any singularities of the Mellin transform function Aω(t). The purely perturbative BFKL formalism generates a Mellin transform function with a cut along the real axis in the ω-plane. However, it has been shown [2] that if the strong coupling runs with the transverse momentum, t, a phase-matching boundary condition is automatically imposed at a value, tc, of t where the t -dependence of Aω(t) changes from an oscillatory function to a decaying one. If, moreover, one assumes that the infrared properties of QCD impose a further constraint on the phase of these oscillations at some small value of transverse momentum, then the two constraints can only be simultaneously satisfied for a discrete set, ωn, of ω, and the singularity structure of Aω(t) becomes a set of poles, akin to Regge poles. In such cases the amplitude A(y,t) may be written
The positions of the poles ωn as well as their residues, depend not only on the infrared phases, selected by the infrared properties of QCD, but also on the precise running of the coupling. In this way, the discrete BFKL formalism acts as a communicator between high and low energy scales and the predictions of these amplitudes with large rapidity gaps are affected by physics beyond the Standard Model (BSM) even at thresholds which are considerably higher than the energies at which such amplitudes are considered. In a recent paper [3] we have suggested that the quality of the fit of low-x structure functions at HERA is significantly improved by the presence of a supersymmmetry threshold at around 10 TeV.
This immediately poses the question as to how the results from the discrete BFKL formalism can match those of a DGLAP analysis [4] in the double leading-logarithm (DLL) limit where both y and t are large, for which the function Aω(t) obeys the DGLAP equation
In the case of the purely perturbative BFKL formalism with a cut singularity in ω, this match is understood [5] from the fact that at large g and small ω, the Mellin transform function from the BFKL analysis is approximated by
which is a solution to eq.(3) and the inverse Mellin transform (1) is dominated by a saddle-point at
2. THE GREEN FUNCTION
The BFKL equation (at leading order) with running coupling is given by
and is solved in terms of a universal (i.e. process independent) Green function, Gω(t,t') which obeys the equation
This Green function is only uniquely defined once certain boundary conditions are imposed. The first of these is the requirement that for physically sensible results
There must also be a condition on the Green function for small t,(t') which is imposed by the infrared properties of QCD.
The kernel, K0(t,t') may be expressed in terms of its Fourier transform
For simplicity, we start with a simplified model in which the characteristic function is a quadratic function of v, i.e.
and writing the leading order running coupling as
the Green function obeys Airy's equation
so that it may be expressed in terms of Airy functions Ai(zω(t)) and Bi(zω(t)), where
This Green function oscillates if t<a/(ωβ0) whereas for t>a/ωβ0, Ai decreases, whereas Bi increases. Thus a Green function, which is finite as t(t')→∞ may be written as
However, this is not unique. A more general solution whch satisfies the ultraviolet boundary conditions is
where
The coefficint cω encodes the infrared properties of QCD and thereby determines the behaviour of the Green function for small t(t').
If we write cω=cot(Ø(ω)), then for sufficiently small t ( zω(t)=0) we have
This has poles whenever Ø(ω)=nπ and these are the Regge poles of the BFKL pomeron. determined by the phase of the oscillatory part of the Green function at small t.
This means that the Green function can be written in terms of a the discrete eigenfunctions, fω(t) of the BFKL operator, αs(t)K0(t,t') with eigenvalues ωn as
The sum generates the discrete poles of the BFKL pomeron but the analytic remainder is crucial for the matching of the t - dependence of the large rapidity-gap amplitudes to DGLAP in the DLL limit.
In the case of the real BFKL characteristic function
the Green function may still be written in terms of Airy functions in the semi-classical approximation (in which the oscillation frequency is treated as a slowly varying function of t). The Green function is once again given by eq.(15), but in this case the argument zω(t) of the Airy functions is given by
where vω(t) is the solution to
and tc is the value of t at which vω(tc)=0. Note that this value of tc depends in the exact nature of the running of the coupling and is therefore sensitive to any thresholds for BSM physics - even for very large values of such thresholds.
3. MATCHING TO DGLAP
For sufficiently large t, vω(t) may be approximated by
and the Airy function, Ai, approximates to
4. APPLICATION TO DEEP INELASTIC SCATTERING
For deep-inelastic scattering t = ln(Q2/Ʌ2), where Q2 is the photon virtuality, and the rapidity y is replaced by ln(1/x). In the BFKL formalism, the unintegrated gluon density, g(x,t) which is derivative w.r.t. t of the gluon density, g(x,t) is given by
where ФP(t) is the impact factor that describes the coupling of the QCD pomeron to the proton and is the only process-dependent factor.
The integral over ω goes over a contour C taken to the right of all the poles of Gω (See Fig. 1).
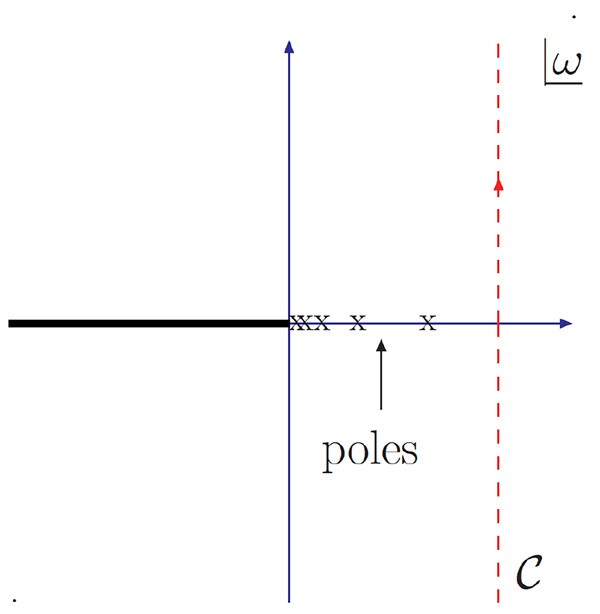 |
Fig. (1). Contour for the inverse mellin transform of the scattering amplitude. |
On the other hand the integrand possesses a saddle-point at ω=ωs given by
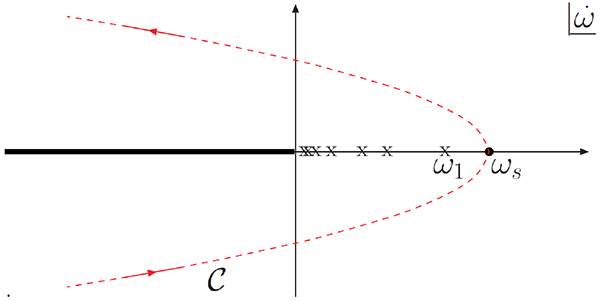 |
Fig. (2). Deformed contour for the inverse Mellin transform of the scattering amplitude in the case where the saddle-point, ωs lies to the right of all the poles of Gω . |
For sufficiently large t, this saddle-point lies to the right of all the poles of Gω (as shown in Fig. 2) i.e.
and the contour may be deformed without crossing a singularity, such that the saddle-point approximation is valid and yields
For large t for which the saddle-point is given by (5), we recover the DGLAP expression on the DLL limit.
The discrete poles affect the overall normalization of the unintegrated gluon density, but not its t -dependence.
However, if t is not sufficiently large then this saddle-point lies to the left of one or more of the poles of Gω (as sown in Fig. 3) and so the saddle-point approximation must be supplemented by the contribution from the contour surrounding these poles, giving rise to an expression for the unintegrated gluon density
 |
Fig. (3). Deformed contour for the inverse Mellin transform of the scattering amplitude in the case where the saddle-point, ωs lies to the left of the leading pole of Gω . |
The contribution from the poles, which does not, in any way, match the DGLAP expression dominates at sufficiently low x. Therefore the DLL limit of DGLAP is not a good approximation in this region of t.
5. SUMMARY
The (discrete) BFKL universal Green function has poles whose positions and residues are controlled by
- The infrared properties of QCD which fixes the phase of the oscillation at small t.
- The precise running of the coupling including the effects of any BSM thresholds.
The Green function consists of a set of poles supplemented by an part which is analytic in ω in such a way that
- For sufficiently large t, when the saddle-point in the inverse Mellin transform lies to the right of all the discrete poles, the t -dependence of the BFKL amplitude matched that of a DGLAP analysis in the DLL limit.
- As t is reduced such that the saddle-point lies to the left of one or more of these poles, the saddle-point approximation for the BFKL amplitude must be supplemented by the contribution from the poles to the right of the saddle-point and a match to a DGLAP analysis is no longer obtained.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflicts of interest.
ACKNOWLEDGEMENS
Declared none.