RESEARCH ARTICLE
NLO BFKL and Anomalous Dimensions of Light-Ray Operators§
Ian Balitsky*
Article Information
Identifiers and Pagination:
Year: 2014Volume: 1
Issue: (Suppl 1: M10)
First Page: 66
Last Page: 71
Publisher Id: PHY-1-66
DOI: 10.2174/1874843001401010066
Article History:
Received Date: 22/11/2013Revision Received Date: 9/12/2013
Acceptance Date: 9/12/2013
Electronic publication date: 31/12/2014
Collection year: 2014
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
Abstract
The anomalous dimensions of light-ray operators of twist two are obtained by analytical continuation of the anomalous dimensions of corresponding local operators. I demonstrate that the asymptotics of these anomalous dimensions at the “BFKL point”. j→1 can be obtained by comparing the light-cone operator expansion with the highenergy expansion in Wilson lines.
PACS number(s): 12.38.Bx, 12.38.Cy.
1. INTRODUCTION
It is well known that the BFKL pomeron [1] gives the anomalous dimensions of leading-twist gluon operators at all orders near the unphysical point with number of covariant derivatives equal to minus one. The exact statement is that the analytical continuation of anomalous dimension of twist-two gluon operator
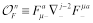 (1)
(1)
to the point
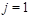 is determined by the BFKL equation. The anomalous dimensions are singular at that point and there is a new hierarchy of perturbation theory
is determined by the BFKL equation. The anomalous dimensions are singular at that point and there is a new hierarchy of perturbation theory
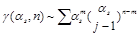 . In the leading order
. In the leading order
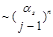 the relation to the BFKL pomeron was established long ago [2] and for the next-to-leading order BFKL it was done in papers [3]. This constitutes a powerful check for explicit calculations of higher-order anomalous dimensions both in QCD [4] and
the relation to the BFKL pomeron was established long ago [2] and for the next-to-leading order BFKL it was done in papers [3]. This constitutes a powerful check for explicit calculations of higher-order anomalous dimensions both in QCD [4] and
 =4 SYM [5]. However, the explicit meaning of these “local operators at the unphysical point” was somewhat obscure. I argue that these operators should be understood as gluon light-ray operators and BFKL equation gives the anomalous dimensions of these light-ray operators at some specific point.
=4 SYM [5]. However, the explicit meaning of these “local operators at the unphysical point” was somewhat obscure. I argue that these operators should be understood as gluon light-ray operators and BFKL equation gives the anomalous dimensions of these light-ray operators at some specific point.
First, let me remind the standard argument about analytical continuation. It is well known that the moments of structure functions are proportional to matrix elements of twist-2 operators. The
 behavior of structure functions are governed by anomalous dimensions of these operators
behavior of structure functions are governed by anomalous dimensions of these operators
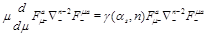 (2)
(2)
As I mentioned, the BFKL pomeron determines the asymptotics of these anomalous dimension at the “non-physical” point
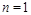 . The standard argument goes like that: in the framework of the BFKL approach the amplitude of, say, virtual
. The standard argument goes like that: in the framework of the BFKL approach the amplitude of, say, virtual
 scattering has the form
scattering has the form
NLO BFKL and Anomalous Dimensions of Light-Ray Operators§ 66
where
 is the pomeron intercept (the explicit form is given by Eq. (41) below) where
is the pomeron intercept (the explicit form is given by Eq. (41) below) where
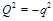 and
and
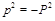 are virtualities of the two photons and
are virtualities of the two photons and
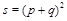 . The case of DIS corresponds to
. The case of DIS corresponds to
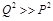 and the Regge limit of small-x DIS to
and the Regge limit of small-x DIS to
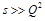
Rewriting this in terms of Bjorken
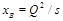 one gets
one gets
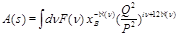 (3)
(3)
which turns to
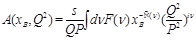 (4)
(4)
after the shift
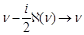 (5)
(5)
The
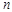 -th moment of the structure function is given by
-th moment of the structure function is given by
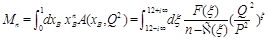 (6)
(6)
where
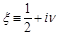 . Now let us consider the integral (6) at
. Now let us consider the integral (6) at
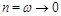 . The contour goes parallel to imaginary axis but we can close it on the poles of the function
. The contour goes parallel to imaginary axis but we can close it on the poles of the function
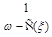 . The expansion of
. The expansion of
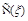 at small
at small
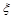 has the form
has the form
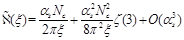
so we get
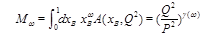 (7)
(7)
where
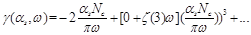 (8)
(8)
Since
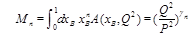 (9)
(9)
we see that the series (8) giver the analytical continuation of the anomalous dimensions of twist-2 operators (1) at the point
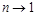 which can be formally denoted as
which can be formally denoted as
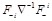 .
.
This method, however, does not tell us the explicit form of this operator and in this paper I will demonstrate that
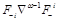 is actually a light-ray operator (
is actually a light-ray operator (
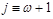 )
)
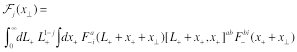 (10)
(10)
and the anomalous dimension of this operator
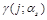 is an analytic continuation of the anomalous dimension (2) of local operators.
is an analytic continuation of the anomalous dimension (2) of local operators.
For simplicity this will be done in
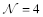 SYM where the conformal invariance simplifies many formulas for the correlation functions. The method to get the anomalous dimensions of the light-ray operator (10) near
SYM where the conformal invariance simplifies many formulas for the correlation functions. The method to get the anomalous dimensions of the light-ray operator (10) near
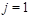 will be to calculate a 4-point correlation function of certain operators in the double “Regge+DIS” limit
will be to calculate a 4-point correlation function of certain operators in the double “Regge+DIS” limit
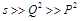 . We will compare two calculations of this 4-point CF: with Regge limit first and DGLAP limit second, or vice versa, and demonstrate that the intercept of the BFKL pomeron
. We will compare two calculations of this 4-point CF: with Regge limit first and DGLAP limit second, or vice versa, and demonstrate that the intercept of the BFKL pomeron
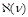 determines the anomalous dimensions in this region. However, first we need to discuss some properties of light-ray operators.
determines the anomalous dimensions in this region. However, first we need to discuss some properties of light-ray operators.
2. LIGHT-RAY OPERATORS
2.1. Light-Ray Operators in Gluodynamics
For simplicity, let us at first look at gluodynamics. For our purposes it is sufficient to consider “forward” light-ray operator
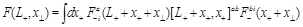 (11)
(11)
Evolution equation for “forward” operators has the form (see e.g. Ref. [6])
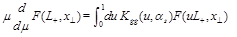 (12)
(12)
Note that since the matrix element of the light-ray operator (11) defines gluon parton density
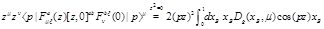
the kernel
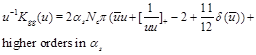 (13)
(13)
is actually a DGLAP kernel (in gluodynamics).
The anomalous dimensions of local twist-2 operators (1) is determined by the kernel (13)
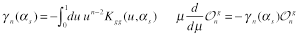 (14)
(14)
Now consider the anomalous dimensions of LR operator (10). Cobining Eqs. (10) and (12) one obtains
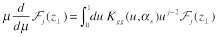
Thus, we see that the anomalous dimension of light-ray operators (11) is an analytical continuation of anomalous dimensions of local operators to non-integer j.
2.2. Singlet light-ray operators in N = 4 SYM
In
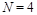 SYM, in addition to the gluon operators (1) there are twist-2 local gluino and scalar operators (as usual, we consider only “forward” highest weight local operators). Similarly to Eq. (11) we can define gluino and scalar light-ray operators (of even parity)
SYM, in addition to the gluon operators (1) there are twist-2 local gluino and scalar operators (as usual, we consider only “forward” highest weight local operators). Similarly to Eq. (11) we can define gluino and scalar light-ray operators (of even parity)
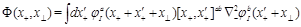
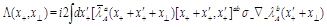
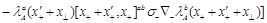
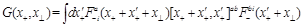 (15)
(15)
The evolution equations have the form similar to (12)
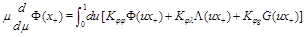
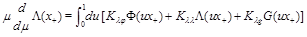
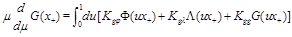 (16)
(16)
where
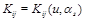 is a function of
is a function of
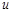 and
and
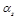 . The expansion in powers of
. The expansion in powers of
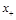 gives anomalous dimensions of local operators
gives anomalous dimensions of local operators
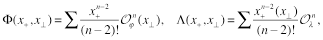
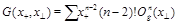 (17)
(17)
where
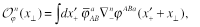
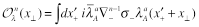
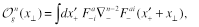 (18)
(18)
Matrix of anomalous dimensions for these “forward” local operators has the form
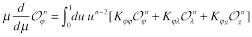
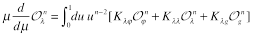
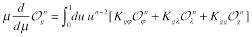 (19)
(19)
The renorm-invariant combinations were found in Ref. [7]:
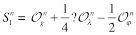
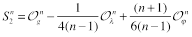
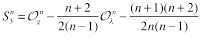 (20)
(20)
The corresponding anomalous dimensions read
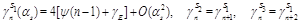 (21)
(21)
Now we define
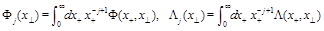
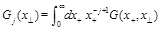 (22)
(22)
From Eq. (16) we get the martix of anomalous dimensions for these LR opertaors
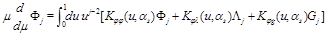
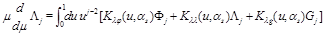
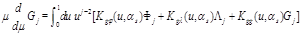 (23)
(23)
Since the matrix (23) is an analytical continuation of the matrix (16) so are the eigenvectors and eigenfunctions and therefore
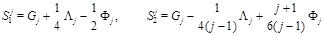
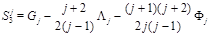 (24)
(24)
are the multiplicatively renormalized operators with anomalous dimensions
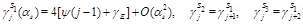 (25)
(25)
Note that at high energy (
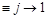 ) only the contribution of
) only the contribution of
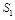 survives because at small
survives because at small
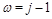 the anomalous dimension of
the anomalous dimension of
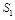 is negative while those of
is negative while those of
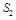 and
and
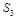 are non-negative and hence we omit contributions of
are non-negative and hence we omit contributions of
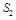 and
and
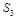 operators in what follows.
operators in what follows.
For future use we need also the operators with the light rays going along the
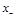 direction defined as
direction defined as
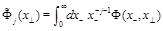 (26)
(26)
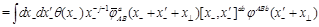
and similarly for
 ,
,
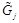 and
and
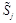 operators.
operators.
3. DGLAP REPRESENTATION OF 4-POINT CORRELATION FUNCTION
To get the anomalous dimensions of light-ray operators (24) near
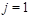 we consider the correlation function of four Konishi operators in the double BFKL + DGLAP limit. Define
we consider the correlation function of four Konishi operators in the double BFKL + DGLAP limit. Define
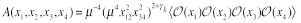 (27)
(27)
where
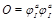 is the Konishi operator (
is the Konishi operator (
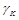 - anomalous dimension). The Regge limit is
- anomalous dimension). The Regge limit is
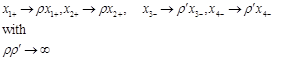 (28)
(28)
and the DGLAP limit corresponds to
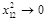 . It is convenient to consider “forward” correlation function
. It is convenient to consider “forward” correlation function
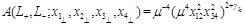 (29)
(29)
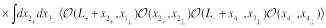
in the double limit: Regge (
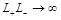 ) plus DGLAP (
) plus DGLAP (
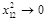 ).
).
First we look at the CF (29) in the DGLAP limit. In this limit we need to expand the product two Konishi operators near the light cone with the leading term being twist-two light-ray operators (24). To get the coefficient functions in this expansion it is convenient to discuss first the three-point
correlation function of a LR operator with two local operators. The correlation function of three local operators is fixed by conformal invariance. In our case it yields
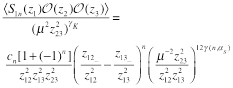 (30)
(30)
For the CF of “forward” operator (15) and two local operators we get
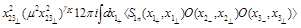 (31)
(31)
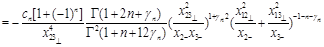
Since a light-ray operator
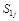 is an “analytical continuation” of a local operator
is an “analytical continuation” of a local operator
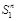 to non-integer
to non-integer
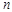 the CF of light-ray operator and two local operators has similar form
the CF of light-ray operator and two local operators has similar form
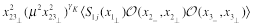 (32)
(32)
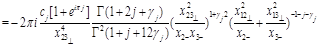
Integrating this over the total translation in
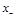 direction we get
direction we get
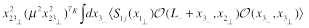
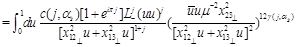 (33)
(33)
To get the expansion of
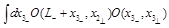 as
as
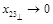 one compares Eq. (33) to the CF of two light-ray operators
one compares Eq. (33) to the CF of two light-ray operators
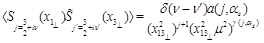 (34)
(34)
One obtains
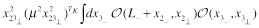
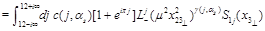 (35)
(35)
It is easy to see that the substitution of Eq. (34) to the r.h.s. of this equation reproduces the 3-point CF (33). Similar result with exchange of
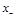 and
and
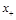 directions reads
directions reads
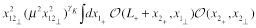
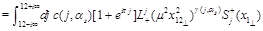 (36)
(36)
Finally, combining the light-cone expansion (36) with the three-point CF (33) we get the “DGLAP representation” of the 4-point CF (29)
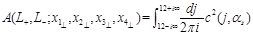
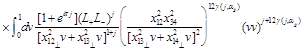 (37)
(37)
In next Section we compare this formula with the “BFKL” representation of the same CF (29).
4. BFKL REPRESENTATION OF 4-POINT CORRELATION FUNCTION
The 4-point CF (27) is a function of two conformal ratios. In the Regge limit (28) it is convenient to choose them as
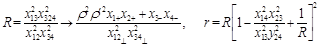
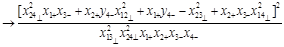 (38)
(38)
It is easy to see that R increases with “energy” (
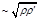 ) while
) while
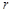 is energy-independent.
is energy-independent.
It was demonstrated that a 4-point CF in
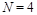 SYM in the Regge limit and at large
SYM in the Regge limit and at large
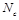 can be parametrized as a contribution of a Regge pole with
can be parametrized as a contribution of a Regge pole with
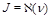
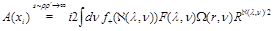 (39)
(39)
where
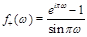 is a signature factor and
is a signature factor and
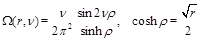 (40)
(40)
is a solution of the Laplace equation in
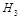 hyperboloid
hyperboloid
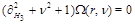 . The dynamics is described by the pomeron intercept
. The dynamics is described by the pomeron intercept
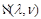 and the “pomeron residue”
and the “pomeron residue”
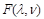 . This formula was proved in [8] (see also [9]) by considering the leading Regge pole in a conformal theory. Also, it was demonstrated up to the NLO level that the structure (39) is reproduced by the high-energy OPE in Wilson lines [10-13].
. This formula was proved in [8] (see also [9]) by considering the leading Regge pole in a conformal theory. Also, it was demonstrated up to the NLO level that the structure (39) is reproduced by the high-energy OPE in Wilson lines [10-13].
The pomeron intercept in
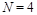 SYM is known in the leading order and in the NLO [14]
SYM is known in the leading order and in the NLO [14]
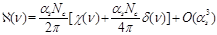 (41)
(41)
We will not need the explicit form of the “pomeron residue”
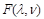 but it can be easily restored from the NLO result for the CF of four protected operators
but it can be easily restored from the NLO result for the CF of four protected operators
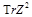 and
and
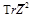 calculated in Ref. [15].
calculated in Ref. [15].
Now let us take the DGLAP limit
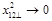 on the top of Regge limit (39). In this limit
on the top of Regge limit (39). In this limit
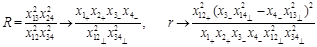
and
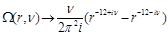 (42)
(42)
so Eq. (39) reduces to
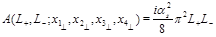
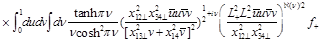
Performing integral over
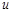 one obtaines the “BFKL” representation of the CF (29) in the double (Regge plus
one obtaines the “BFKL” representation of the CF (29) in the double (Regge plus
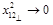 ) limit:
) limit:
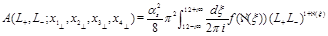
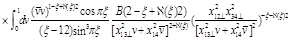 (43)
(43)
where
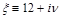 .
.
5. ANOMALOUS DIMENSIONS OF LIGHT-RAY OPERATORS
Let us compare integrals (37) and(43) for the correlation function (27). In both cases, the integrals run parallel to the imaginary axis but the singularities of the integrands lie on the negative real axis. We can close the integrals around negative real axis and compare the integrands near
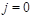 and
and
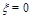 . We see that the integrands coincide if one makes an identification
. We see that the integrands coincide if one makes an identification
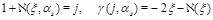 (44)
(44)
and
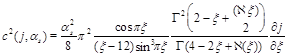 (45)
(45)
If we write down the NLO pomeron intercept (41) as a Laurent series near
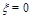
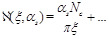 (46)
(46)
we can invert equations (44) and get anomalous dimension near
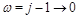 as a series in
as a series in
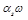
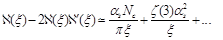
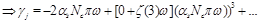 (47)
(47)
In principle, the inversion of Eqs. (44) gives all orders in
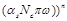 but in practice one gets the first few terms since the analytical form of the inversion is not known.
but in practice one gets the first few terms since the analytical form of the inversion is not known.
It is worth noting that the second of Eqs. (44) corresponds to the shift (5)
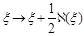 (48)
(48)
in the integral (43). In the momentum space this shift comes from the change of the energy scale from the symmmetric
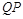 to non-symmetric
to non-symmetric
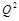 while in the coordinate space it comes directly from the symmetric “energy scale” R, see Eq. (38).
while in the coordinate space it comes directly from the symmetric “energy scale” R, see Eq. (38).
CONFLICT OF INTEREST
The author confirms that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This work was supported by contract DE-AC05-06OR23177 under which the Jefferson Science Associates, LLC operate the Thomas Jefferson National Accelerator Facility.