RESEARCH ARTICLE
Timelike vs Spacelike DVCS from JLab, Compass to Ultraperipheral Collisions and AFTER@LHC§
H. Moutarde1, B. Pire2, F. Sabatié1, L. Szymanowski*, 3, J. Wagner3
Article Information
Identifiers and Pagination:
Year: 2014Volume: 1
Issue: Suppl 1: M8
First Page: 57
Last Page: 61
Publisher Id: PHY-1-57
DOI: 10.2174/1874843001401010057
Article History:
Received Date: 15/6/2013Revision Received Date: 27/9/2013
Acceptance Date: 2/10/2013
Electronic publication date: 31/12/2014
Collection year: 2014
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
Abstract
Timelike and spacelike virtual Compton scattering in the generalized Bjorken scaling regime are complementary tools to access generalized parton distributions. We stress that the gluonic contributions are by no means negligible, even in the medium energy range which will be studied intensely at JLab12 and in the COMPASS-II experiment at CERN. Ultraperipheral collisions with proton or ion beams may also be used at RHIC and at collider or fixed target experiments at LHC.
1. INTRODUCTION
In the collinear factorization framework the scattering amplitudes for exclusive processes such as deeply virtual Compton scattering (DVCS) [1]
1
and its crossed reaction, timelike Compton scattering (TCS) [2]
2
have been shown to factorize in specific kinematical regions, provided a large scale controls the separation of short distance dominated partonic subprocesses and long distance hadronic matrix elements, the generalized quark and gluon distributions (GPDs) [3] which encode much information on the partonic content of nucleons. After factorization, the DVCS (and similarly TCS) amplitudes are written in terms of Compton form factors (CFF) , and , , as:
3
with the CFFs defined as:
4
We report in Sect. 2 on a recent NLO analysis [4, 5] of DVCS and TCS amplitudes, and make a few remarks on the study of TCS in ultraperipheral collisions at hadron colliders (Sect. 3) and at fixed target experiments at LHC (Sect. 4).
2. ON THE IMPORTANCE OF GLUONIC CONTRIBUTIONS
2.1. Gluonic Effects to Compton form Factors
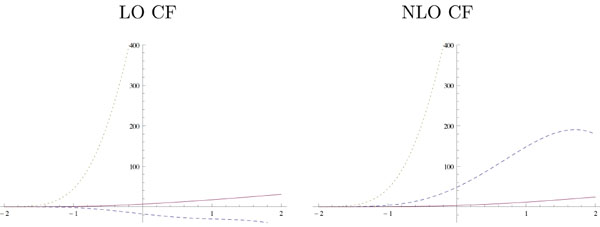
TCS and DVCS amplitudes are identical (up to a complex conjugation) at lowest order in αs but differ at next to leading order, in particular because of the quite different analytic structure of the scattering amplitudes of these reactions. Indeed, the production of a timelike photon enables the production of intermediate states in some channels which are kinematically forbidden in the DVCS case. This opens the way to new absorptive parts of the amplitude. To estimate Compton Form Factors (CFF), we use the NLO calculations of the coefficient functions which have been calculated in the DVCS case in the early days of GPD studies and more recently for the TCS case [4], the two results being simply related thanks to the analyticity (in Q2) properties of the amplitude [6]:
5
where + (–) sign corresponds to vector (axial) case.
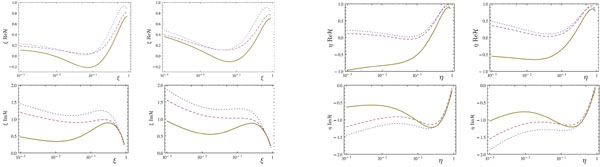
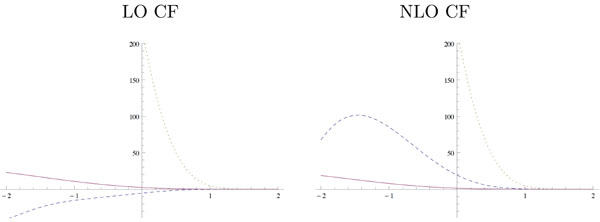
Using two GPD models based on Double Distributions (DDs), as discussed in detail in [5]: the Goloskokov-Kroll (GK) model [7] and a model based on the MSTW08 PDF parametrization [8], we get the results shown in Fig. (1) for the real and imaginary parts of the spacelike and timelike dominant CFF H(ξ,t) and H(η,t). Comparing dashed and solid lines in the upper panels, one sees that gluonic contributions are so important that they even change the sign of the real part of the CFF, and are dominant for almost all values of the skewness parameter. A moderate result arises from a similar comparison of the lower panels; the gluonic contribution to the imaginary part of the CFF remains sizeable for values of the skewness parameter up to 0.3.
2.2. Gluonic Effects to DVCS Observables
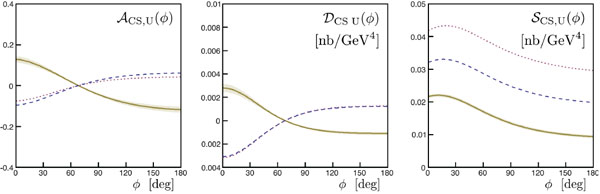
The effects of NLO contributions to some of the DVCS observables at moderate energies are exemplified in Figs. (2, 3) which show specific observables to be measured at JLab and COMPASS. The difference between the dotted and solid lines demonstrates that NLO contributions are important, whereas the difference between the dashed and solid lines shows that gluon contributions should not be forgotten even at low energy when a precise data set is analyzed.
3. TCS IN ULTRAPERIPHERAL COLLISIONS
Timelike Compton scattering in ultraperipheral collisions at hadron colliders opens a new way to measure generalized parton distributions, in particular for very small values of the skewness parameter.
We estimated [9] the different contributions to the lepton pair cross section for ultraperipheral collisions at the LHC. Since the cross sections decrease rapidly with Q2, we are interested in the kinematics of moderate Q2, say a few GeV2, and large energy, thus very small values of η. Note however that for a given proton energy the photon flux is higher at smaller photon energy.
The Bethe-Heitler amplitude grows much when small θ angles are allowed. In the following we will use the limits [π/4,3π/4] where the Bethe-Heitler cross section is sufficiently big but does not dominate too much over the Compton process. The Bethe-Heitler cross section integrated over θ∈[π/4,3π/4],ϕ∈[0,2π], Q2∈[4.5,5.5]Gev2,|t|∈[0.05,0.25]Gev2, as a function of γp energy squared s is in the limit of large s constant and equals 28.4 pb.
Since the amplitudes for the Compton and Bethe-Heitler processes transform with opposite signs under reversal of the lepton charge, the interference term between TCS and BH is odd under exchange of the ℓ+ and ℓ- momenta. It is thus possible to project out the interference term through a clever use of the angular distribution of the lepton pair. The interference part of the cross-section for with unpolarized protons and photons has a characteristic (θ,ϕ) dependence given by (see details in [9]).
with
where , and H H E are Compton form factors. With the integration limits symmetric about θ=π/2 the interference term changes sign under ϕ→π+ϕ due to charge conjugation, whereas the TCS and BH cross sections do not. One may thus extract the Compton amplitude through a study of .
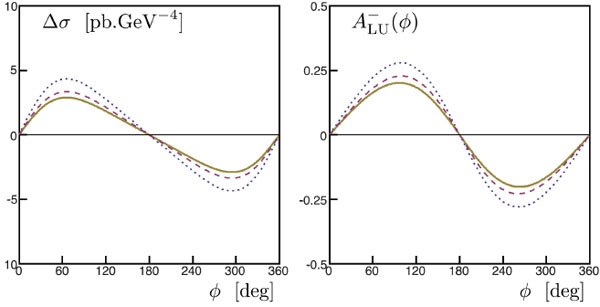
The lepton pair production differential cross sections (solid lines) for , integrated over , as a function of ϕ, for (a) (b) with . We also display the Compton (dotted), Bethe-Heitler (dash-dotted) and Interference (dashed) contributions.
In Fig. (4) we show the interference contribution to the cross section in comparison to the Bethe-Heitler and Compton processes, for various values of photon proton energy squared . We observe that for larger energies the Compton process dominates, whereas for all contributions are comparable.
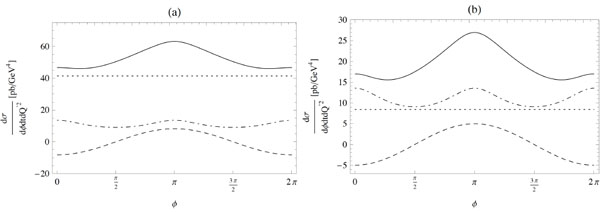 |
Fig.(4). The lepton pair production differential cross sections (solid lines) for t = –0.2GeV2, Q2 = 5GeV2 integrated over θ = [π/4; 3 π/4], as a function of φ, for s = 107GeV2 (a) s = 105 GeV2 (b) with μF2 = 5GeV2. We also display the Compton (dotted), Bethe-Heitler (dash-dotted) and Interference (dashed) contributions. |
4. ULTRAPERIPHERAL COLLISIONS IN A HIGH-ENERGY FIXED-TARGET EXPERIMENT AFTER@ LHC
The main idea of the multi-purpose project AFTER@LHC is to extract the halo of the LHC proton or ion beams by means of a bent-cristal and to use it as a beam in the fixed-target experiments [10]. The extracted beams will have a sufficiently high energy to produce on fixed target in ultraperipheral scattering a lepton pair with high invariant mass or heavy mesons. In these experiments a nucleus projectile or a nucleus target is treated as a high-energy photon source which allows study of photon-hadron collisions. Figs. (5 and 6, respectively) shows preliminary estimates of the Bethe-Heitler, TCS, and Interference contributions to the cross section, as functions of the CMS rapidity y, after integration over
, in the region where the interference contribution is best seen, for the collision of a proton beam with a pb target (and of a pb beam with a proton target respectively). The double distribution model of GPDs based on MSTW08 parametrization is used.
SUMMARY AND OUTLOOK
We did not discuss here the rich phenomenology of DVCS and TCS processes which electron-ion colliders [11] will allow to study. Neither did we comment on recent progresses in higher twist contributions [12] nor on the effect of resummation of higher order QCD corrections [13]. The physics of generalized parton distributions is definitely a domain of work in progress, both on the theory and on the experimental side.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflicts of interest.
ACKNOWLEDGMENTS
This work is supported by the Polish Grant NCN No DEC-2011/01/B/ST2/03915, the French-Polish collaboration agreement Polonium, the ANR project "Partons", the COPIN-IN2P3 Agreement and the Joint Research Activity "Study of Strongly Interacting Matter" (HadronPhysics3, Grant Agreement no. 283286) under the 7th Framework Programme of the European Community.