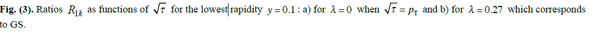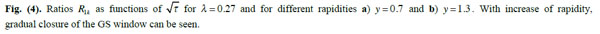This talk based on refs. [1-6] (where also an extensive list of references can be found) follows closely an earlier report of ref. [7]. We shall discuss the scaling law, called geometrical scaling (GS), which has been introduced in the context of DIS [8]. It has been also shown that GS is exhibited by the p_T spectra at the LHC [1, 3] and that an onset of GS can be seen in heavy ion collisions at RHIC energies [3]. At low Bjorken x < x_max gluonic cloud in the proton is characterized by an intermediate energy scale Q_s (x), called saturation scale [9, 10]. Q_s (x) is defined as the border line between dense and dilute; gluonic systems (for review see e.g. refs. [11, 12]). In the present paper we study the consequences of the very existence of Q_s (x); the details of saturation phenomenon are here not of primary importance.

Here we shall focus of four different pieces of data which exhibit both emergence and violation of geometrical scaling. In Sect. 2 we briefly describe the method used to assess the existence of GS. Secondly, in Sect. 3 we describe our recent analysis [4] of combined HERA data [13] where it has been shown that GS in DIS works surprisingly well up to relatively large x_max~0.1 (see also [14]). Next, in Sect. 4, on the example of the CMS p_T spectra in central rapidity [15], we show that GS is also present in hadronic collisions. For particles produced at non-zero rapidities, one (larger) Bjorken x=x₁ may be outside of the domain of GS, i.e.x₁>x_max, and violation of GS should appear. In Sect. 5 we present analysis of the pp data from NA61/SHINE experiment at CERN [16] and show that GS is indeed violated once rapidity is increased. Finally in Sect. 6 we analyze identified particles spectra where the particle mass provides another energy scale which may lead to the violation of GS, or at least to some sort of its modification [6]. We conclude in Sect. 7.

Geometrical scaling hypothesis means that some observable σ depending in principle on two independent kinematical variables, like x and Q², depends in fact only on a given combination of them, denoted in the following as τ:

Here function F in Eq. (1) is a dimensionless universal function of scaling variable τ:

and

is the saturation scale. Here Q₀ and x₀ are free parameters which, however, are not of importance in the present analysis, and exponent λ is a dynamical quantity of the order of λ ~ 0.3. Throughout this paper we shall test the hypothesis whether different pieces of data can be described by formula (1) with constantλ, and what is the kinematical range where GS is working satisfactorily.

As a consequence of Eq. (1) observables σ(x_i,Q²) for different x_i's should fall on a universal curve, if evaluated in terms of scaling variable τ. This means that ratios

should be equal to unity independently of τ. Here for some x_ref we pick up all x_i < x_ref which have at least two overlapping points in Q².

For λ≠0 points of the same Q² but different x's correspond in general to different τ's. Therefore one has to interpolate σ(x_ref,τ(x_ref,Q²;λ)) to Q²_k,ref such that τ(x_ref,Q²_k,ref;λ)=τ_k. This procedure is described in detail in ref. [4].

By adjusting λ one can make R_xi,xref(λ;τ_k)→ 1 for all τ_k in a given interval. In order to find an optimal value λ_min which minimizes deviations of ratios (4) from unity we form the chi-square measure

where the sum over k extends over all points of given x_i that have overlap with x_ref, and N_xi,xref is a number of such points.

In the case of DIS the relevant scaling observable is γ^{* p} cross section and variable x is simply Bjorken x. In Fig. (1) we present 3-d plot of λ_min(x,x_ref) which has been found by minimizing (5).

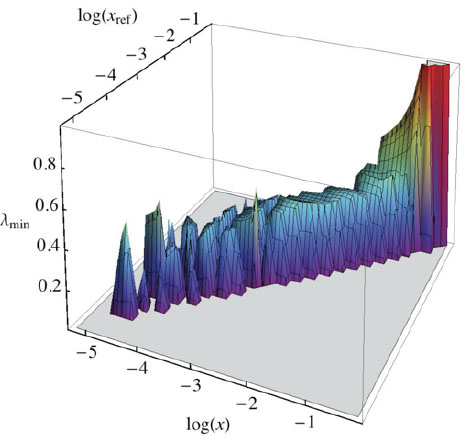Fig.(1). Three dimensional plot of λmin(x, xref) obtained by minimization of Eq. (5).

Qualitatively, GS is given by the independence of λ_min on Bjorken x and by the requirement that the respective value of χ²_x,xref(λ_min) is small (for more detailed discussion see ref. [4]). One can see from Fig. (1) that the stability corner of λ_min extends up to x_ref~0.1, which is well above the original expectations. In ref. [4] we have shown that:

In hadronic collisions at c.m. energy W=s particles are produced in the scattering process of two patrons (mainly gluons) carrying Bjorken x's

For central rapidities x=x₁ ~ x₂ In this case charged particles multiplicity spectra exhibit GS [1]

where F is a universal dimensionless function of the scaling variable (2). Therefore the method of ratios can be applied to the multiplicity distributions at different energies (W_i taking over the role of x_i in Eq. (4))¹. For W_ref we take the highest LHC energy of 7 TeV. Hence one can form two ratios R_Wref,Wi with W₁ = 2.36 and W₂ = 0.9 TeV. These ratios are plotted in Fig. (2) for the CMS single non-diffractive spectra for λ = 0 and for λ = 0.27, which minimizes (5) in this case. We see that original ratios plotted in terms of p_T range from 1.5 to 7, whereas plotted in terms of they are well concentrated around unity. The optimal exponent λ is, however, smaller than in the case of DIS. Why this so, remains to be understood.

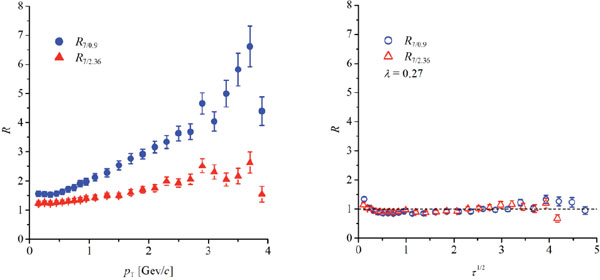Fig.(2).

For y > 0 two Bjorken x's can be quite different: x₁ > x₂. Therefore by increasing y one can eventually reach x₁ > x_max and GS violation should be seen. For that purpose we shall use pp data from NA61/SHINE experiment at CERN [16] at different rapidities y = 0.1-3.5 and at five scattering energies W_1,...,5 = 17.28, 12.36, 8.77, 7.75 , and 6.28 GeV.

In Fig. (3) we plot ratios R_1i = R_W1,Wi (4) for π^- spectra in central rapidity for λ = 0 and 0.27. For y = 0.1 the GS region extends down to the smallest energy because x_max is as large as 0.08. However, the quality of GS is the worst for the lowest energy W₅. By increasing y some points fall outside the GS window because x₁ ≥ x_max, and finally for y ≥ 1.7 no GS is present in NA61/SHINE data. This is illustrated nicely in Fig. (4).

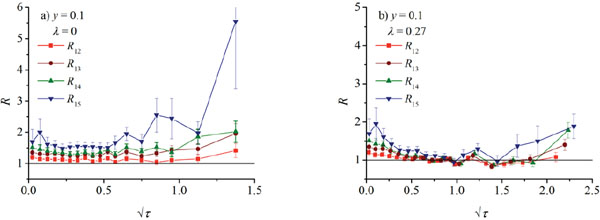Fig.(3).

Fig.(4).

In ref. [6] we have proposed that in the case of identified particles another scaling variable should be used in which p_T is replaced by mT=mTm=mT2+mT2m(mTscaling), i.e.

This choice is purely phenomenological for the following reasons. Firstly, the gluon cloud is in principle not sensitive to the mass of the particle it finally is fragmenting to, so in principle one should take p_T as an argument of the saturation scale. In this case the proper scaling variable would be

However this choice (mT=pT – scaling) does not really differ numerically from the one given by Eq. (9).

To this end let us see how scaling properties of GS are affected by going from scaling variable τ_pT = τ (2) to mT (9) and what would be the difference in scaling properties if we had chosen p_T as an argument in the saturation scale leading to scaling variable mTpT (10). This is illustrated in Fig. (5) where we show analysis [6] of recent ALICE data on identified particles [17]. In Fig. (5a-c) full symbols refer to the p_T – scaling (2) and open symbols to mT – scaling or mTp_T – scaling. One can see very small difference between open symbols indicating that scaling variables mT (9) and mTpT (10) exhibit GS of the same quality. On the contrary p_T – scaling in variable τ_pT(2) is visibly worse.

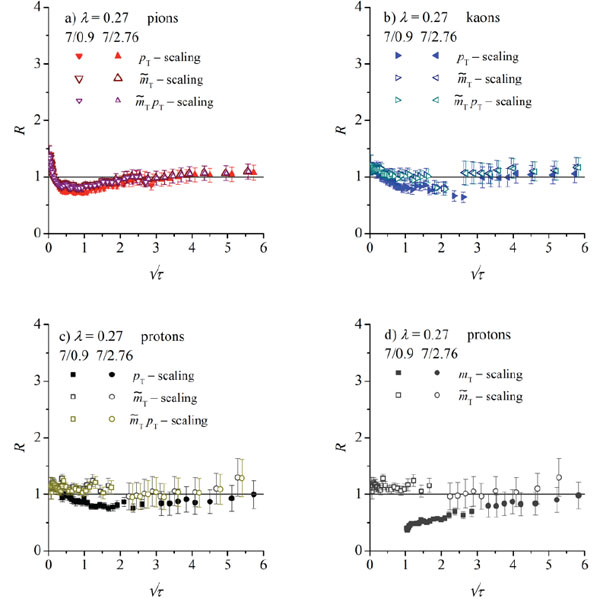Fig.(5).

Finally in Fig. (5d), on the example of protons, we compare mT – scaling (open symbols) and m_T – scaling (full symbols) in variable

for λ =0. 27. One can see that no GS has been achieved in the latter case. Qualitatively the same behavior can be observed for other values of λ.

In ref. [4] we have shown that GS in DIS works well up to rather large Bjorken x's with exponent λ = 0.32-0.34. In pp collisions at the LHC energies in central rapidity GS is seen in the charged particle multiplicity spectra, however, λ = 0.27 in this case [1]. By changing rapidity one can force one of the Bjorken x's of colliding patrons to exceed x_max and GS violation is expected. Such behavior is indeed observed in the NA61/SHINE pp data [5]. Finally we have shown that for identified particles scaling variable τ of Eq. (2) should be replaced by mT defined in Eq. (9) and the scaling exponent λ ≈0.3 [6].

The authors confirm that this article content has no conflicts of interest.